Resumen
El conocimiento y monitoreo de los precios del mercado inmobiliario se consideran necesarios para la implementación de políticas públicas y la gestión territorial, así como una fuente genuina de recursos para el Estado. Sin embargo, las diferentes características y dinámicas territoriales demandan procesos y técnicas que posibiliten la actualización adecuada y eficiente a cada realidad. El presente documento describe las técnicas y resultados obtenidos para la valuación masiva de la tierra de la provincia de Córdoba, particularmente en localidades serranas de perfil turístico. Se analiza el desempeño de la técnica de aprendizaje automático Quantile Regression Forest, en términos del nivel de precisión para predecir el valor de la tierra y se presentan las estructuras de valor resultantes. Además, la principal innovación de la técnica propuesta consiste en la posibilidad de generar un mapa de la consistencia de la predicción, en términos del coeficiente de dispersión en cada punto del espacio. Esta última característica se considera un insumo clave en la implementación de políticas públicas de actualización periódica de los valores fiscales de la tierra urbana, al informar sobre posibles áreas de la ciudad en donde los resultados son de mayor o menor calidad en relación al entorno.
Palabras claves: valor de la tierra urbana, valuación masiva, aprendizaje automático, árbol de regresión cuantílica
Abstract
Knowledge and monitoring land values are necessary for the implementation of public policies and territorial management, as well as a genuine source of resources for local governments. However, the different territorial characteristics and dynamics demand adequate processes and techniques for each reality. This paper describes the techniques and results obtained for the massive valuation of land in the province of Córdoba, particularly in mountain localities with a tourist profile. The performance of the Quantile Regression Forest machine learning technique is analyzed in terms of the level of accuracy in predicting land value and the resulting value structures are presented. In addition, the main innovation of the proposed technique consists in the possibility of generating a map of the prediction consistency, in terms of the dispersion coefficient at each point of the space. This last feature is considered a key input in the implementation of public policies for the periodic updating of urban land tax values, by informing about possible areas of the city where the results are of higher or lower quality in relation to the surroundings.
Key Words: urban land value, mass appraisal, machine learning, quantile regression forest
Fecha de recepción: 14 de octubre de 2021
Fecha de aceptación: 22 de noviembre de 2021
Introducción
La generación de conocimiento público y abierto sobre el valor de la tierra en diferentes puntos del espacio brinda luz en mercados inmobiliarios tradicionalmente opacos, de funcionamiento ineficiente a causa de diferentes asimetrías de información. Además, tiene múltiples efectos positivos en la gestión territorial por parte de los gobiernos locales y en la manera que se relacionan con la ciudadanía.
La desactualización de las valuaciones fiscales, en un contexto inflacionario recurrente como el de Argentina, trae aparejadas diversas desventajas. Desde el punto de vista de la política fiscal, se generan efectos nocivos sobre la equidad del impuesto inmobiliario recaudado por los gobiernos locales. La inequidad impositiva puede dividirse en horizontal y vertical, donde la primera se entiende como una situación en la cual dos contribuyentes con igual capacidad de pago son gravados de forma diferente por el Estado. Morales Schechinger (2007) explica este fenómeno de una manera más completa: el mercado de la tierra está en constante movimiento, donde coexisten alteraciones estructurales que afectan en la misma magnitud a los precios de todos los terrenos, junto con alteraciones particulares que sólo afectan a terrenos específicos. No registrar la evolución urbana en las valuaciones fiscales durante un amplio período de tiempo genera una estructura de bases imponibles regresivas, ya que se gravan de manera más laxa áreas urbanas más dinámicas y se castiga comparativamente más a aquellas zonas que se han vuelto menos dinámicas, o cuyo atractivo inmobiliario disminuyó con el paso del tiempo. Esta situación se traduce en una elevada falta de equidad horizontal del sistema tributario local (Morales Schechinger, 2007). Por su parte, la equidad vertical desaparece en el momento que dos contribuyentes de diferente capacidad contributiva son gravados de igual manera por el Estado. Se observa que las ciudades consolidadas de América Latina presentan una elevada segregación urbana (Sabatini, 2003), donde el crecimiento se configura hacia la periferia debido a la segregación auto-inducida de los grupos de alto poder adquisitivo y la segregación por expulsión de los sectores de bajos recursos (Cervio, 2015). Estos dos universos suelen coexistir en espacios urbanos acotados, que emergieron sobre tierra vacante de uso previamente rural y de valor fiscal bajo. Una estructura de valuaciones obsoleta que no registre esta dinámica en el valor del suelo en estas nuevas áreas urbanas, implica gravar de igual manera a dos universos de contribuyentes que, a pesar de compartir el mismo espacio urbano, se encuentran en la realidad segregados, cayendo en una inequidad vertical (Carranza, et al., 2019).
Desde el punto de vista del desarrollo territorial de las ciudades y la planificación urbana, el desconocimiento o desactualización de los valores de la tierra fomenta la retención de tierras y la especulación inmobiliaria. Siguiendo a Morales Schechinger (2007): “La retención de tierras es un ejemplo de conducta patrimonialista en la que participan todo tipo de propietarios cuando el entorno del mercado es desregulado y desgravado”, situación que se traduce en grandes espacios vacíos que, al ser rodeados por la dinámica urbana, cuentan con acceso a múltiples servicios públicos típicamente urbanos. El costo de oportunidad de estos espacios fragmentados es doble: no sólo se pone de manifiesto la contradicción entre zonas de viviendas precarias habitadas por hogares hacinados y grandes áreas urbanas vacantes que suele ser resuelta mediante procesos de ocupación informal de estos espacios, sino que se encarece la provisión de bienes y servicios públicos que deben sortear espacios vacíos para cumplir con su finalidad.
Adicionalmente, la inversión pública y el accionar de los gobiernos locales generan cambios en los usos del suelo. Estas externalidades son capturadas en el valor de la tierra, siendo necesario mantener actualizado el valor fiscal del suelo urbano para implementar estrategias impositivas de recuperación de plusvalías. El cambio en el patrón de uso, obras de infraestructura y equipamientos, entre otras, son ejemplos de aumentos del valor del suelo dados por alguna acción pública (Morales Schechinger, 2007). Estos factores generan incrementos en el valor de la tierra por causas ajenas a los propietarios del suelo, aunque también se vean beneficiados. Capturar esta revalorización es fundamental para fortalecer el financiamiento local y el desarrollo socioeconómico de las ciudades (Reese, 2003).
Estos patrones y características espaciales tienen una correlación directa con la mayor o menor valorización de los inmuebles y sus entornos. Así no solo cada ciudad, sino los diferentes sectores dentro de ésta presentan estructuras de valores que es necesario conocer para aportar a la equidad territorial, fiscal y tributaria.
La heterogeneidad territorial de la provincia de Córdoba, presenta un desafío en este sentido, con más de 400 localidades de escalas y roles diversos. Desde la ciudad Capital hasta pequeños poblados; ciudades mayoritariamente vinculadas a la actividad agropecuaria, industrial, así como otras con rol principal turístico.
En las localidades urbanas en donde el turismo representa una parte considerable de la actividad económica, los aspectos mencionados anteriormente tienen el potencial de encontrarse exacerbados. El hecho de que diferentes puntos del espacio sean un “atractivo turístico” impacta sobre el valor del suelo del entorno, generando extensiones urbanas destinadas a la renta inmobiliaria que, a medida que se expanden, expulsan a la población original hacia la periferia. Esta situación genera grandes entornos urbanos de elevado valor y totalmente cubiertos por bienes y servicios públicos de calidad que permanecen deshabitados fuera de temporada, en contraste dialéctico con áreas periféricas de marcadas carencias, y en donde habita la población que se trabaja en el sector turístico de dicha localidad.
Por lo tanto, el diseño de instrumentos que permitan a los diferentes niveles del Estado implementar políticas de actualización de los valores fiscales de la tierra urbana da cuenta de que el conocimiento territorial desde el propio Estado es un elemento central y potencial para la gestión y la implementación de políticas de suelo y del ordenamiento territorial en general (Smolka y Mullahy, 2010). Asimismo, este tipo de políticas constituyen un aporte a la recuperación de la inversión pública, así como facilitan la identificación de zonas con mayor o menor valorización y las variables que las determinan, a fin de definir intervenciones públicas que promuevan un desarrollo territorial con mayor equidad urbana y un mejor financiamiento de las ciudades.
Las iniciativas de actualización de los valores fiscales suelen generar altos costos económicos y políticos para los funcionarios que deciden llevarlas a cabo, y el margen de error inherente al proceso de implementación suele frustrar los intentos de implementación, llevando a una desactualización sistémica de los valores fiscales.
Sin embargo, algunas ciudades latinoamericanas, entre ellas Córdoba (Egino y Erba, 2020), se han dado las tareas de generar nuevos mapas de valores, actualizar los valores catastrales y modelar el funcionamiento del mercado de suelo, haciendo uso de nuevas metodologías y tecnologías, como estrategia sostenible y sistemática hacia la modernización catastral y la promoción de mejores políticas. En este sentido la generación de grandes volúmenes de información sistematizada, los progresos computacionales y generalización de información georreferenciada a partir de la masificación de satélites orbitando la tierra, han impactado de manera positiva en la generación de tecnologías aplicadas en el diseño de políticas urbanas en diferentes partes del mundo. Durante los últimos 10 años ha sido notable el desarrollo de algoritmos de aprendizaje automático (machine learning) para la predicción de fenómenos urbanos, entre ellos la determinación de los valores de la tierra.
En base a lo anterior, y entendiendo la valuación masiva como un mecanismo de estimación a gran escala, el presente trabajo busca evaluar la aplicación del algoritmo Quantile Regression Forest para estimar el valor de la tierra en un conglomerado de localidades turísticas de las sierras de Córdoba, Argentina. Se analiza el desempeño de la técnica de valuación masiva propuesta en términos del nivel de precisión con la cual se logra predecir el valor de la tierra, y las posibles ventajas en la generación de mapas que informen sobre la distribución espacial de la precisión del modelo, permitiendo conocer no sólo la tasa de error general que usualmente acompaña a investigaciones de este tipo, sino también la focalización en aquellas en las cuales el riesgo de obtener valuaciones erróneas es más elevado. Se considera que el aporte realizado en este último punto es clave para la implementación exitosa de políticas de actualización de los valores fiscales, ya que brinda información que permite una mejor gestión del riesgo en su implementación. Se espera, por lo tanto, aportar a la producción de conocimiento y al diseño de herramientas que tiendan a una implementación más acertada e informada de políticas de actualización del valor del suelo urbano.
Algoritmos de aprendizaje automático: Quantile Regression Forest
El modelo de aprendizaje automático Quantile Regression Forest (QRF) (Meinshausen, 2006) es una adaptación del algoritmo Random Forest (RF) (Breiman, 2001). A su vez, RF es una generalización del árbol de clasificación y regresión (CART) (Breiman et al. 1984). CART permite describir la variable de estudio (output), mediante medidas de posición y dispersión, clasificar y jerarquizar en función de un conjunto de variables explicativas (inputs), e inferir qué valores puede asumir el output cuando se desconoce su valor, pero se tiene información relacionada a los inputs utilizados. Este tipo de metodología presenta un excelente ajuste para los datos de entrenamiento o muestrales. Sin embargo, al momento de predecir con nuevos datos lo hace de manera imprecisa, producto de un sobreajuste (“overfitting”) de los datos, derivando en errores por elevada varianza (Hastie et al., 2009).
Para solucionar los problemas de overfitting, surge la idea de ensamblado, que busca entrenar distintos modelos usando el mismo algoritmo de aprendizaje (Porras Garrido, 2016), con el objetivo de reducir simultáneamente el sesgo y la varianza. Algunas técnicas de ensamblado utilizados son Bagging, Boosting y Stacking (Breiman, 1996).
La técnica de Bagging consiste en tomar submuestras de igual tamaño, aleatorias y con reposición de la muestra original (Breiman et al. 1984). Sobre cada submuestra se entrena un mismo algoritmo de aprendizaje automático. Posteriormente, cada uno de estos diferentes modelos, entrenados a partir de diferentes submuestras de la muestra original, se utiliza para predecir el output para un nuevo conjunto de datos. Las predicciones de cada modelo se promedian, alcanzando resultados con mejor ajuste, mitigando así el sesgo y la varianza. CART es un excelente candidato para este tipo de técnicas de ensamblado, ya que captura estructuras de interacción compleja y tiene sesgo bajo a medida que el árbol crece lo suficiente (Hastie et al., 2009).
RF es la aplicación de bagging a la modelización mediante CART. Se combinan los árboles de regresión para formar un “bosque”, de manera tal que cada árbol dependa de los valores de un vector aleatorio, independiente e idénticamente distribuido. Dado que cada árbol del bosque aleatorio se construye con un procedimiento similar, el sesgo del promedio de los árboles es muy parecido al sesgo de cada árbol individual, es decir, cada árbol del bosque tiene la misma distribución (Hastie et al., 2009). Por lo tanto, los árboles son forzados a ser diferentes aleatoriamente mediante la selección contingente de las variables explicativas, reduciendo de esta forma la correlación del bosque. De esta forma, al promediar árboles no correlacionados se obtienen ganancias en términos de varianza, reduciendo así el overfitting. Dado que la predicción de RF se conforma del promedio de las predicciones de todos los árboles que lo forman (Amat, 2020), este algoritmo brinda una aproximación precisa de la media condicionada de la variable respuesta (Meinshausen, 2006).
El algoritmo
QRF, desarrollado por Meinshausen (2006), que es una adaptación del algoritmo
Random Forest, sigue la misma estrategia de ensamblado, aunque varía la
agregación de las predicciones resultantes de cada árbol. QRF permite realizar
predicciones no sólo de la media condicionada (como el RF), sino también del
resto de los cuantiles (Amat, 2020). Es decir, se amplía la información
brindada por RF, permitiendo obtener información sobre la distribución total
condicional de la variable respuesta, y no únicamente de la media condicionada
(Meinshausen, 2006). Por lo tanto, con este algoritmo se puede predecir la
mediana en lugar de la media, brindando una mayor robustez en presencia de
outliers. Adicionalmente, este algoritmo puede utilizarse para identificar
áreas donde la predicción tenga mayor varianza (Amat, 2020). La desviación
estándar de la predicción en cada punto ![]() puede estimarse a
partir del límite inferior y superior del intervalo de predicción del 68,27%
(Hengl et al., 2018), como puede apreciarse en la ecuación (1):
puede estimarse a
partir del límite inferior y superior del intervalo de predicción del 68,27%
(Hengl et al., 2018), como puede apreciarse en la ecuación (1):
|
|
(1) |
Los valores de ![]() pueden expresarse en
términos de la mediana y así conformar un aproximado del coeficiente de
dispersión (CD).
pueden expresarse en
términos de la mediana y así conformar un aproximado del coeficiente de
dispersión (CD).
Configuración de la muestra de observaciones del Mercado Inmobiliario y selección del área de estudio
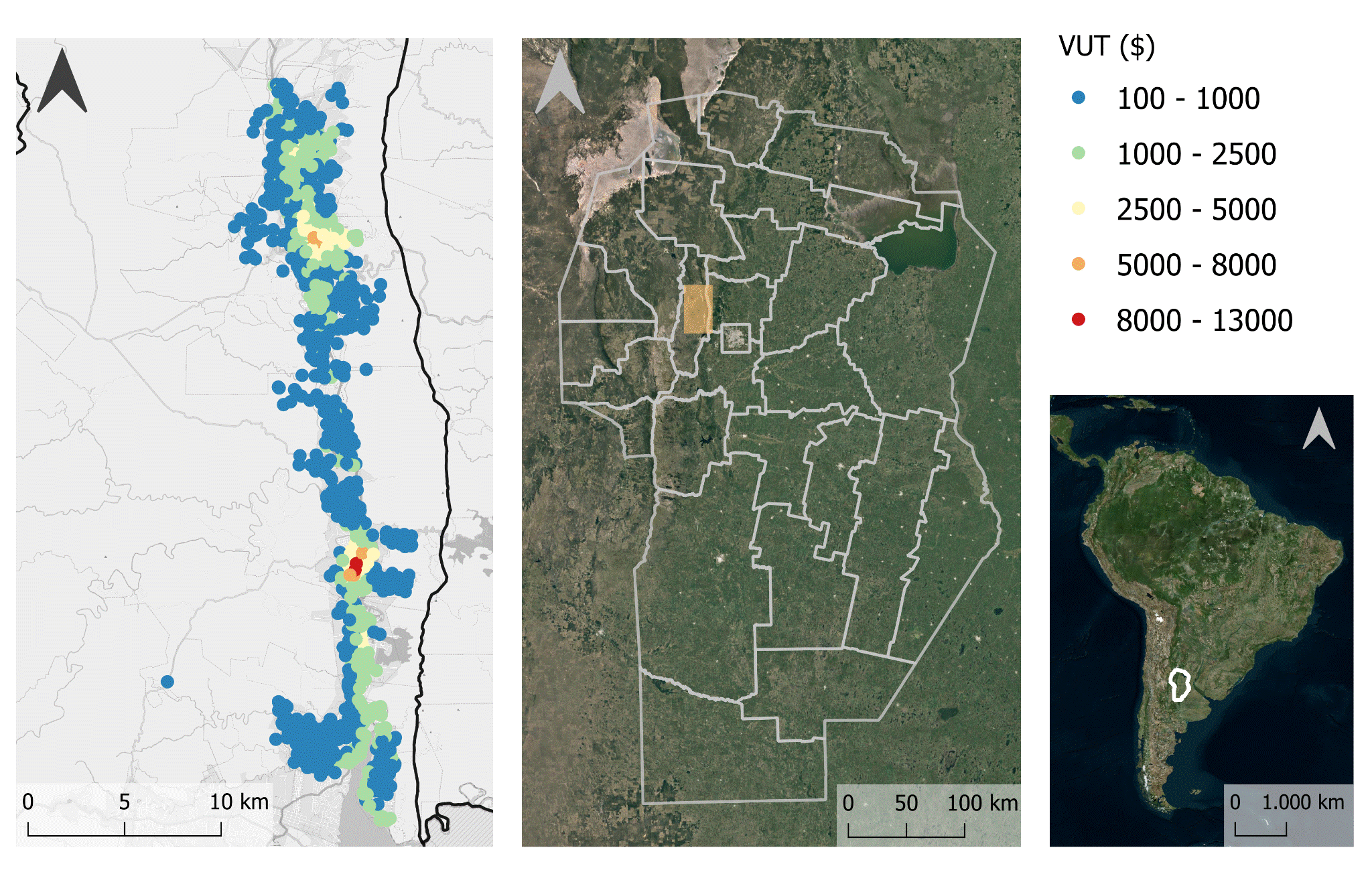
El área de estudio fue conformada por las localidades ubicadas sobre la Ruta Nacional N°38, al noroeste de la capital provincial (Ciudad de Córdoba): Bialet Massé, Casa Grande, Cosquín, Huerta Grande, La Falda, San Roque, Santa María de Punilla, Valle Hermoso y Villa Giardino. Correspondiendo este corredor a uno de los principales sectores turísticos de la provincia. En total, este sector cuenta con 92.242 parcelas urbanas cuyo valor del suelo se predijo mediante el algoritmo Quantile Regression Forest.
Considerando una muestra 1.031 datos del mercado inmobiliario, relevados durante los años 2018, 2019 y 2020, (Mapa 1) registrados en el Observatorio del Mercado Inmobiliario (OMI) de la Provincia de Córdoba[1]. Las características de dichas observaciones son muy diversas: coexisten valores de parcelas con amplias superficies y otros lotes muy pequeños; parcelas cuyo frente es muy estrecho, con otras de frente amplio; datos relevados en distintos momentos del tiempo y a tipos de cambio entre el peso y el dólar diferentes; predios con diferentes ubicaciones en la cuadra (medial, esquina, interno, salida a dos calles); formas rectangulares y regulares, en conjunto con irregulares; valores de venta y de oferta, en donde se asume que los valores de oferta tienen un margen de negociación implícito que es necesario descontar; parcelas con situación jurídica regular junto con predios sin escrituras[2]. De esta manera, los datos relevados en el mercado inmobiliario no son directamente comparables entre sí. Esta heterogeneidad hace necesario aplicar un proceso de homogeneización a los fines de su procesamiento conjunto.
Siguiendo un procedimiento análogo al detallado en Bullano et al. (2020) y Cerino et al. (2020), utilizando técnicas de econometría espacial se estima un modelo lineal con el objetivo de obtener elasticidades que permitan descontar los efectos sobre el valor por metro cuadrado de las variaciones en el tipo de cambio vigente al momento del relevamiento de cada observación, la superficie, ancho de frente, forma, ubicación en la cuadra, tipo de valor y situación jurídica, con el objetivo de obtener valores homogéneos comparables entre sí. En Argentina esto es particularmente relevante, ya que una parte importante del mercado inmobiliario se encuentra dolarizado, y los episodios de devaluación de la moneda son frecuentes. Una vez descontados los efectos de las particularidades de cada observación muestral, se define la variable de estudio para el presente artículo: el valor unitario de la tierra urbana (VUT), consistente en el valor por metro cuadrado de suelo para una parcela de 500 metros cuadrados, con 10 metros de frente, de forma regular, ubicación en la cuadra medial, correspondiente a una venta concretada (se descuenta el margen de negociación típico de los valores en oferta). con escritura, y expresado a mayo de 2020 (punto temporal medio de la distribución).
El Mapa 1 refleja la ubicación del aglomerado, así como la distribución geográfica de las muestras de mercado.
Mapa 1: Área de estudio (izq) y Distribución geográfica de la muestra de mercado (der)
Fuente: Elaboración Propia
En la Tabla 1 se presentan las estadísticas descriptivas del valor unitario de la tierra (en pesos argentinos correspondientes a mayo de 2020). El VUT promedio en el aglomerado asciende a $1.061 m², mientras que la mediana es menor ($748 m²). Las localidades de La Falda y Santa María de Punilla presentan las medianas más altas ($1.166 m² y $1.119 m² respectivamente). La Falda también es la localidad con el VUT máximo; sin embargo, para la localidad de Santa María de Punilla esto no es así, es más el máximo VUT de esta localidad es bajo en relación al resto de las localidades, indicando una estructura de valor estable. Cosquín resalta entre los máximos ($10.421 m²) pero presenta una mediana relativamente baja ($583 m²) denotando una estructura de valor diferente.
|
Media ($/m²) |
Mediana ($/m²) |
Min. ($/m²) |
Max. ($/m²) |
Obs. |
|
|
BIALET MASSÉ |
670,37 |
486,26 |
108,41 |
2.199,09 |
135 |
|
CASA GRANDE |
597,47 |
572,85 |
191,21 |
1.611,85 |
61 |
|
COSQUÍN |
1.145,55 |
583,23 |
214,07 |
10.421,43 |
195 |
|
HUERTA GRANDE |
881,15 |
778,29 |
132,93 |
4.131,49 |
104 |
|
LA FALDA |
2.030,58 |
1.165,83 |
206,36 |
12.764,21 |
128 |
|
SAN ROQUE |
913,69 |
859,96 |
488,78 |
1.753,00 |
77 |
|
SANTA MARIA DE PUNILLA |
1.209,12 |
1.118,86 |
384,80 |
2.869,56 |
55 |
|
VALLE HERMOSO |
724,53 |
659,17 |
157,82 |
1.588,06 |
100 |
|
VILLA GIARDINO |
1.036,76 |
947,94 |
239,35 |
2.995,94 |
176 |
|
TOTAL |
1.060,78 |
747,69 |
108,41 |
12.764,21 |
1.031 |
Tabla 1: Estadísticas descriptivas del VUT por localidad.
Fuente: Elaboración Propia
Además de las muestras de valores de la tierra, se generó un conjunto de variables independientes con el objetivo de capturar características territoriales externas a las propiedades intrínsecas de cada parcela, que puedan afectar su valor por metro cuadrado. Estas variables pueden clasificarse en dos grupos: de distancia y de entorno. Las primeras se calcularon en base a métodos cartográficos mediante el uso de sistemas de información geográfica, como por ejemplo distancia a redes viales, cursos de agua, zonas de mayor o menor categoría, entre otras.
Por su parte, las variables de entorno se construyeron principalmente en base a datos catastrales, procesamiento de imágenes satelitales, y análisis de proximidad, considerando un radio de análisis dado por la autocorrelación espacial del valor del suelo, definido en 500 metros lineales, a partir del rango de un semivariograma empírico. Así, se determinaron variables como porcentaje de metros cuadrados edificados en relación a la cantidad total de metros cuadrados de terreno (indicador del grado de consolidación del entorno), porcentaje de parcelas baldías en relación al total de parcelas en el radio (indicador del stock de predios vacantes en el sector), etc.
Además del valor por metro cuadrado actualizado y homogeneizado, cada entrada en la base de datos utilizada tiene la siguiente información: Distancia a rutas (d_ruta); Distancia a vías principales (d_viasprin); Distancia a vías secundarias (d_viassec); Distancia a ríos (d_rio); Distancia a zonas de alto valor (d_alta); Distancia a zonas de bajo valor (d_baja); Distancia a zonas de depreciación de valor (d_depre); Distancia a líneas divisorias de valor (d_lineadiv); Cantidad total de baldíos en un entorno de 500 m de radio (perc_bald); Cantidad total de metros cuadrados de baldíos en un entorno de 500 m de radio (perc_baldm); Cantidad de edificados sobre la cantidad de en un entorno de 500 m de radio (perc_edif); Tamaño promedio de los predios en un entorno de 500 m de radio (prom_predio); Índice de vegetación de diferencia normalizada: estima cantidad, calidad, densidad y desarrollo de la vegetación (ndvi); Índice Urbano: mide la densidad de edificación por pixel (ui); Índice de Radios Normalizados de Suelo Desnudo: enfoque empírico para resaltar las cubiertas del suelo de la vegetación y las superficies impermeables. Identifica composición y cobertura del suelo determinado a partir de humedad y brillo (rndsi); Índice de Composición Biofísica, dado por la presencia vegetación, suelo impermeable y suelo desnudo (bci); Índice de construcción de diferencia normalizada: estima zonas con superficies edificadas (consolidadas) o en desarrollo (sin consolidar) respecto a zonas con vegetación o desnudas (ndbi); Porcentaje de píxeles construidos en un radio de 500 m (ind_con); Porcentaje Urbano Edificado Compacto (porc_uec); Porcentaje Urbano Edificado Disperso (porc_ued); Porcentaje Rural Edificado (porc_re); Porcentaje Espacio Abierto Urbano (porc_eau); Porcentaje Borde Urbano (porc_bu); Porcentaje Espacio Abierto Rural (porc_ear); Porcentaje Agua (porc_agua); Índice que mide el grado de fragmentación urbana establecido en cuatro niveles, describe la configuración espacial a partir del análisis de pixeles edificados (fragment); Variable categórica que indica la localidad a la que pertenece la observación (localidad); longitud (x); latitud (y).
Las estadísticas descriptivas de las variables independientes se pueden observar en la Tabla 2.
|
Min |
Primer Q |
Mediana |
Media |
Tercer Q |
Max |
|
|
d_ruta |
12,00 |
577,50 |
1102,00 |
1259,95 |
1839,00 |
4683,00 |
|
d_viasprin |
16,00 |
388,50 |
924,00 |
1101,29 |
1655,00 |
5000,00 |
|
d_viassec |
12,00 |
154,00 |
398,00 |
635,26 |
867,00 |
5000,00 |
|
d_alta |
0,00 |
694,50 |
1138,00 |
1282,13 |
1707,00 |
5000,00 |
|
d_baja |
0,00 |
371,00 |
806,00 |
892,27 |
1269,50 |
5000,00 |
|
d_lineadiv |
16,00 |
190,50 |
522,00 |
687,55 |
963,50 |
5000,00 |
|
d_depre |
0,00 |
868,00 |
1534,00 |
1765,35 |
2564,00 |
5000,00 |
|
d_rio |
8,00 |
333,50 |
690,00 |
820,72 |
1150,50 |
2942,00 |
|
prom_edif |
0,00 |
17,73 |
43,47 |
59,00 |
84,87 |
300,31 |
|
prom_predio |
332,00 |
638,50 |
878,00 |
1082,89 |
1129,50 |
31726,00 |
|
perc_edif |
0,00 |
0,02 |
0,04 |
1,75 |
0,11 |
147,51 |
|
perc_baldm |
0,02 |
0,41 |
0,65 |
0,60 |
0,81 |
1,00 |
|
perc_bald |
0,04 |
0,41 |
0,65 |
0,61 |
0,84 |
1,00 |
|
porc_uec |
0,00 |
0,00 |
0,00 |
0,52 |
0,00 |
54,97 |
|
porc_ued |
0,00 |
0,00 |
0,00 |
5,72 |
7,41 |
42,45 |
|
porc_re |
0,00 |
0,80 |
2,03 |
2,42 |
3,75 |
9,50 |
|
porc_eau |
0,00 |
0,00 |
0,00 |
16,94 |
36,58 |
84,29 |
|
porc_bu |
0,00 |
0,00 |
0,00 |
2,64 |
6,07 |
13,84 |
|
porc_ear |
0,00 |
41,64 |
90,08 |
69,73 |
97,20 |
100,00 |
|
porc_agua |
0,00 |
0,00 |
0,00 |
2,03 |
0,00 |
34,63 |
|
bci |
1,32 |
1,72 |
1,77 |
1,77 |
1,84 |
2,07 |
|
rndsi |
1,40 |
2,05 |
2,23 |
2,21 |
2,37 |
3,15 |
|
ui |
-0,62 |
-0,44 |
-0,38 |
-0,39 |
-0,34 |
-0,13 |
|
ndbi |
-0,33 |
-0,15 |
-0,10 |
-0,11 |
-0,06 |
0,06 |
|
ndvi |
0,17 |
0,44 |
0,47 |
0,47 |
0,52 |
0,65 |
|
ind_con |
0,00 |
0,02 |
0,05 |
0,09 |
0,10 |
0,67 |
|
fragment |
1,00 |
2,00 |
3,00 |
2,57 |
3,00 |
4,00 |
Tabla 2: Estadísticas descriptivas de las variables independientes.
Fuente: Elaboración Propia
Resultados
Con el objeto de evaluar la capacidad predictiva del algoritmo QRF en cada localidad se utiliza la metodología de validación cruzada (cross-validation). El primer paso consiste en dividir la muestra de manera aleatoria en diez partes de igual tamaño (o similar tamaño en caso de que la muestra tenga una cantidad de observaciones impar). A continuación, se retira de la muestra una de estas partes, para ser utilizada como una base de prueba o “testing”. Las restantes nueve submuestras conforman la base de entrenamiento o “training”. Se estima el modelo QRF con los datos de la base “training” y para medir el nivel de precisión se predicen los datos del grupo extraído “testing”. El procedimiento continúa de manera iterativa hasta que cada uno de los diez grupos fue evaluado fuera de la muestra. De esta manera se obtiene una base de igual tamaño que la muestra inicial, pero incluyendo el valor predicho para cada observación. Así, se puede agrupar esta información por localidad, y obtener el nivel de precisión del modelo para cada localidad del aglomerado.
Para medir el nivel de precisión del modelo QRF se acude al error relativo promedio en valor absoluto (MAPE, por sus siglas en inglés), que es una medida estándar en la bibliografía y se define de la siguiente manera:
|
|
(2) |
Donde, ![]() es el valor predicho
por el modelo para la observación
es el valor predicho
por el modelo para la observación ![]() , cuando se encuentra fuera
de la muestra,
, cuando se encuentra fuera
de la muestra, ![]() es el valor real de la
observación
es el valor real de la
observación ![]() y
y ![]() es la cantidad de
datos en la muestra.
es la cantidad de
datos en la muestra.
Los errores por localidad se pueden apreciar en lal Tabla 3. El MAPE promedio en todo el aglomerado fue de 18,57%. La variabilidad del MAPE entre localidades no es alta, indicando un máximo de 23% en la localidad de Huerta Grande, y un mínimo de 13% en Valle Hermoso.
|
MAPE (%) |
Observaciones |
|
|
BIALET MASSÉ |
21,35% |
135 |
|
CASA GRANDE |
20,78% |
61 |
|
COSQUÍN |
17,23% |
195 |
|
HUERTA GRANDE |
23,37% |
104 |
|
LA FALDA |
19,69% |
128 |
|
SAN ROQUE |
13,99% |
77 |
|
SANTA MARIA DE PUNILLA |
20,84% |
55 |
|
VALLE HERMOSO |
13,12% |
100 |
|
VILLA GIARDINO |
17,88% |
176 |
|
TOTAL |
18,57% |
1.031 |
Tabla 3: MAPE por localidad.
Fuente: Elaboración Propia
Conocido el MAPE para cada localidad, se procede al entrenamiento del algoritmo QRF en toda la muestra de mercado, para luego realizar las predicciones sobre la base parcelaria.
Además del nivel general de error del modelo aplicado a nivel de localidad, se procedió a calcular el coeficiente de dispersión (CD) del algoritmo para cada parcela predicha. Es decir, en la predicción de cada parcela intervinieron 500 árboles de decisión, y se tomó la mediana los valores predichos por cada uno de ellos como VUT predicho en dicha localización. De igual manera, se tomó coeficiente de dispersión de las predicciones de todos los árboles como una medida de la cohesión del valor predicho para esta parcela. En el límite, si todos los árboles coinciden con el valor predicho para una parcela, el coeficiente de dispersión allí será igual a cero. Esta estrategia posibilitó obtener un CD para cada parcela en la base de datos, y mapear esta variable para conocer su distribución espacial, indicando áreas en donde los resultados fueron más robustos y otras en donde la dispersión de los resultados fue más elevada.
A continuación, se presentan una serie de figuras que indican los mapas del VUT predicho y el CD para cada parcela de dos de las localidades más relevantes del área de estudio: Cosquín y La Falda. Adicionalmente se agrega la ubicación de las muestras de mercado, sólo a efectos interpretativos.
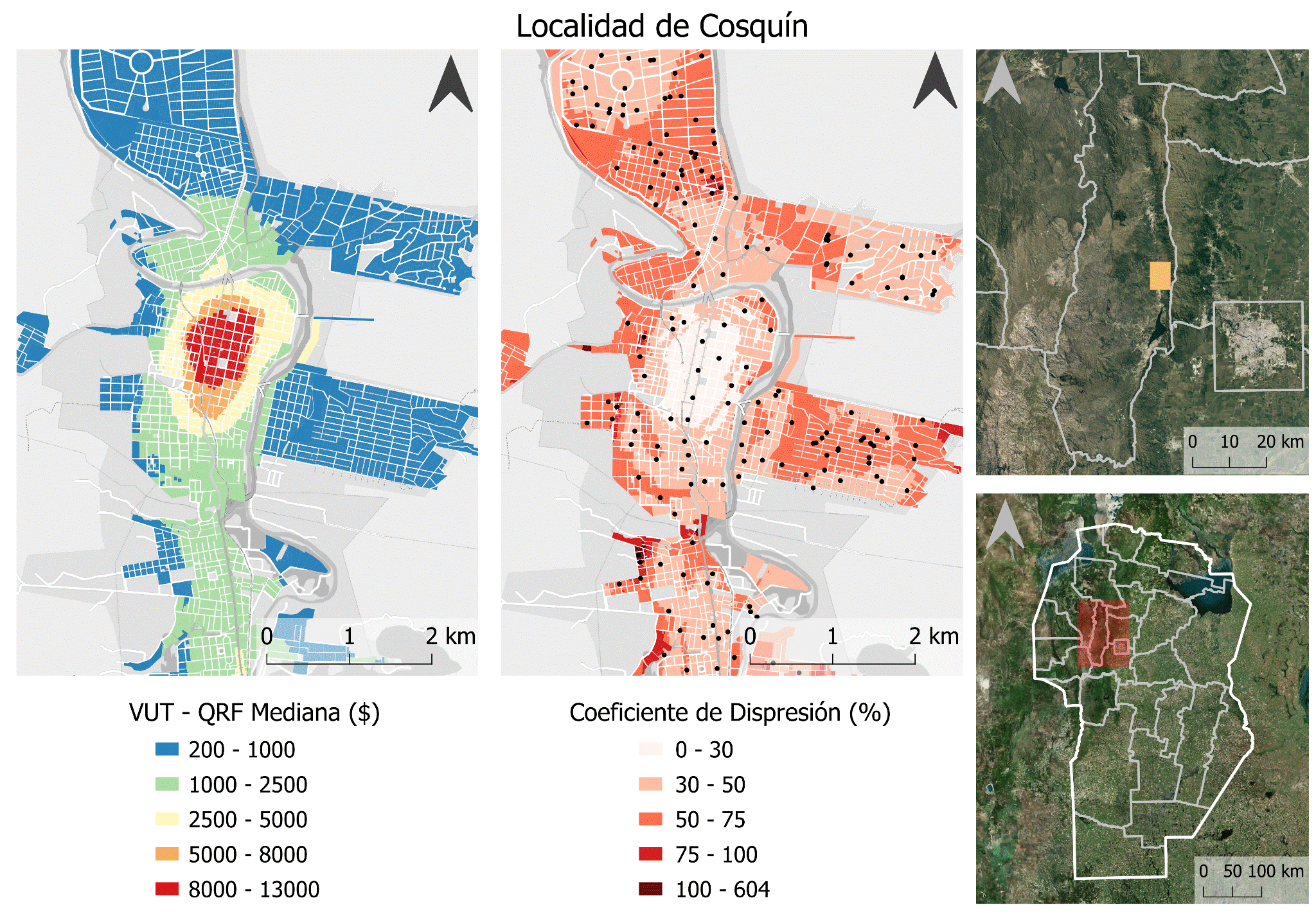
El mapa de valor y de dispersión de la Localidad de Cosquín puede observarse en el Mapa 2. La estructura de valor de la tierra en Cosquín presenta un pico de valor en el centro de la localidad y va disminuyendo concéntricamente a medida que se aleja de esta zona de alta valuación. Esta zona central concentra la actividad recreativa, gastronómica, de alojamiento y de atractivo turístico de esta localidad, mejor accesibilidad y consolidación urbana. Por su parte, el segundo y tercer anillo en la estructura se aproxima al río, considerado también un elemento de atracción en una localidad serrana y vacacional como lo es Cosquín. Finalmente, la localidad muestra un crecimiento por extensión en sentido Norte-Sur apoyada por la Ruta 38 sobre todo hacia el sur donde se evidencia una conurbación con otras localidades serranas y proximidad a Carlos Paz, una de las principales localidades turísticas de la provincia de Córdoba.
Respecto al CD, se aprecia que las zonas con mayor dispersión en la predicción de cada árbol del bosque aleatorio se encuentran en la periferia, en las zonas con menores cantidades de observaciones muestrales o en aquellas zonas con quiebres en el valor del suelo, principalmente cuando se pasa de valores máximos (indicado con rojo) a valores más bajos (amarillo). Estos cambios en la estructura del valor del suelo hacen que las predicciones sean más variables en las parcelas que se encuentran en medio de estos cambios.
Mapa 2: Mapa de valor y de dispersión en la base parcelaria.
Fuente: Elaboración Propia
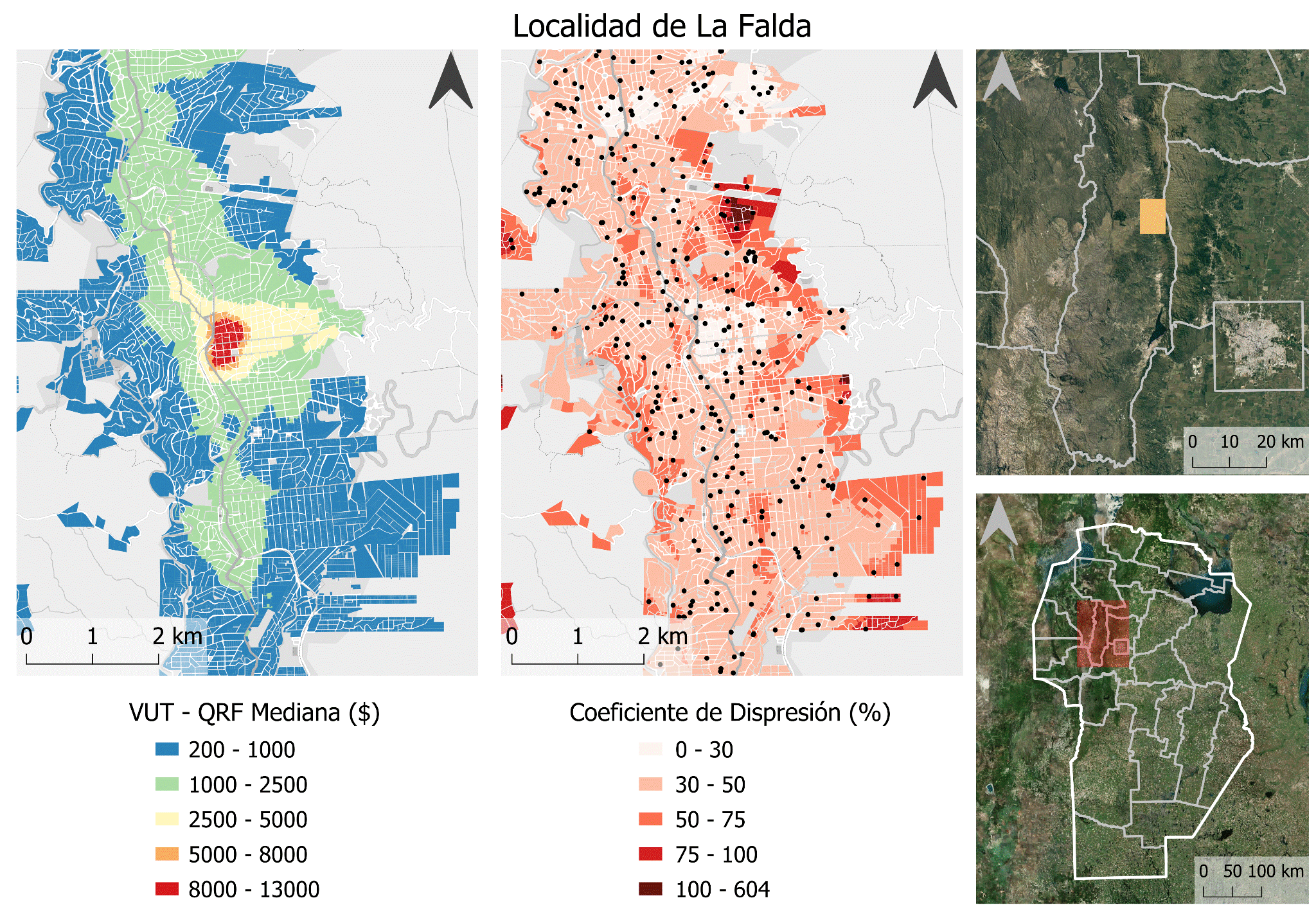
En el Mapa 3 se puede apreciar que La Falda presenta una estructura de valor similar a la de Cosquín, una centralidad con un máximo de valor que disminuye en todas direcciones a medida que se aleja de él. En esta localidad, si bien la concentración de actividades recreativas, comerciales, gastronómicas, de alojamiento, etc., se concentran en el centro geográfico de la ciudad localizado sobre la ruta 38 como principal acceso, se extienden en sentido este-oeste a partir de la Avenida Edén y 9 de julio como principales ejes comerciales y recreativos de la localidad. También, en sentido similar a Cosquín, la conurbación con otras localidades de perfil turístico caracteriza el siguiente escalón en la estructura resultante.
Los patrones del CD parecen ser similares a los de la localidad de Cosquín. En los quiebres de valor, en la periferia de la ciudad y en los lugares con menor cantidad de observaciones de mercado la estabilidad del modelo es menor.
Mapa 3: Mapa de valor y de dispersión en la base parcelaria.
Fuente: Elaboración Propia
Conclusiones
El objetivo del presente artículo consistió en presentar una metodología para la valuación masiva de la tierra urbana, junto con una estimación de la distribución espacial de la consistencia de la estimación. En primer lugar, una metodología ágil que permita obtener estimaciones del valor de la tierra a partir de una muestra de mercado de pocas observaciones (en este artículo se utilizaron 1.031 datos de mercado para predecir el valor de la tierra en 92.242 parcelas urbanas, un 1,1% del total), facilita la implementación regular de políticas de actualización masiva del valor fiscal de la tierra. Una política de este estilo permitiría comenzar a visualizar no sólo cuál es el valor de la tierra en determinados sub-espacios urbanos, sino cómo es la dinámica que rige al fenómeno, identificando qué factores contribuyen o limitan el aumento de los valores de la tierra. Además, desde el punto de vista de los costos asociados a este tipo de iniciativas, la diferencia entre este tipo de metodologías con los amplios operativos de campo al estilo de los avalúos realizados hasta la década de 1990 es notable. En segundo lugar, la generación de un mapa que informe sobre el nivel de coherencia interna de la estimación se constituye en una herramienta crítica en la implementación de este tipo de políticas por parte de los gobiernos locales, ya que permite identificar áreas potenciales de reclamos por parte de los ciudadanos, permitiendo una gestión del costo político más adecuada y facilitando la implementación y evaluación de este tipo de iniciativas.
Los resultados fueron satisfactorios, el MAPE para todo el aglomerado estuvo en torno al 18%, el mínimo, que se corresponde con la localidad de Valle Hermoso, se ubicó en 13%, y el máximo (en Huerta Grande) en 23%. Dadas las características del algoritmo QRF fue posible obtener una medida de desviación estándar de la predicción para cada parcela. Dividiendo la desviación estándar por la mediana de las estimaciones se generó una medida de desvío expresada como porcentaje del valor predicho para cada punto de la base parcelaria. Las zonas identificadas con mayor variabilidad se relacionan con menor cantidad de datos muestrales, la periferia de las ciudades, y límites de cambios de valor.
En función de los resultados obtenidos, se observa que la utilización de métodos de aprendizaje automáticos reduce en gran manera los tiempos que conllevan una valuación masiva y contribuyen en la generación de información que permiten controlar de manera más acotada los posibles errores de estimación. Estas dos características facilitan la implementación de políticas de actualización periódica del valor de la tierra urbana, en un contexto en donde las alteraciones en los precios de las propiedades inmobiliarias sufren cambios constantes.
Referencias
Amat Rodrigo, J. (2020). Regresión cuantílica: Quantile regression forest. https://www.cienciadedatos.net/documentos/53_regresion_cuantilica_quantile_regresion_forest.html.
Anselin, L. (1995). Local indicators of spatial association—LISA. Geographical analysis, 27(2), 93-115.
Bezdek, J. C., Ehrlich, R., & Full, W. (1984). FCM: The fuzzy c-means clustering algorithm. Computers & Geosciences, 10(2-3), 191-203.
Bonet, J. A., Muñoz, A., Mannheim, C. R. P., & Torres, F. S. (2014). El potencial oculto: Factores determinantes y oportunidades del impuesto a la propiedad inmobiliaria en América Latina. Banco Interamericano de Desarrollo.
Breiman, L., Friedman, J., Stone, C., and Olshen, R. (1984). Classification and Regression Trees. CRC press.https://doi.org/10.1201/9781315139470
Breiman, L. (1996). Bagging predictors. Machine Learning, 24(2), 123–140. ttps://doi.org/10.1007/BF00058655
Breiman, L. (2001). Random forests. Machine learning, 45(1), 5–32. https://doi.org/10.1023/A:1010933404324
Bullano, M. E., Carranza, J. P., Piumetto M. A., Cerino R. M., Monzani F., & Córdoba M. A. (2020). El impacto de las variaciones del tipo de cambio sobre el valor de la tierra urbana. ¿El mercado inmobiliario está totalmente dolarizado? Asociación Argentina de Economía Política. Reunión Anual 2020. https://aaep.org.ar/anales/works/works2020/Bullano.pdf
Carranza, J. P., Piumetto, M., Salomón, M., Monzani, F., Montenegro, G., & Córdoba, M. (2019). Valuación masiva de la tierra urbana mediante inteligencia artificial: El caso de la ciudad de San Francisco, Córdoba, Argentina. Revista Vivienda y Ciudad, (6), 90–112. https://revistas.unc.edu.ar/index.php/ReViyCi/article/view/27090/28749
Cerino R. M., Carranza, J. P., Piumetto M. A., Bullano, M. E., Monzani F., y Córdoba M. A. (2020). Homogeneización de valores de la tierra mediante técnicas de econometría espacial en valuaciones masivas automatizadas. Congreso de Catastro Multifinalitario y Gestión Territorial. Florianópolis, Brasil.
Cervio, A. L. (2015). Expansión urbana y segregación socio-espacial en la ciudad de Córdoba (Argentina) durante los años ‘80. Astrolabio (14), 360–392. https://revistas.unc.edu.ar/index.php/astrolabio/article/view/10610
De Cesare, C. M. (2012). Improving the performance of the property tax in Latin America. Cambridge, MA: Lincoln Institute of Land Policy.
Eguino, H. y Erba, D. (Eds.). (2020). Catastro, valoración inmobiliaria y tributación municipal. https://publications.iadb.org/es/catastro-valoracion-inmobiliaria-y-tributacion-municipal-experiencias-para-mejorar-su-articulacion
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Springer Science & Business Media.
Hengl, T., Nussbaum, M., Wright, M.N., Heuvelink, G.B.M., Gräler, B., 2018. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 6, e5518. https://doi.org/10.7717/peerj.5518
Marshall, A. (1890). Principles of economics Macmillan. London (8th ed. Published in 1920).
Meinshausen, N. (2006). Quantile regression forests. Journal of Machine Learning Research, 7(Jun), 983–999.https://www.jmlr.org/papers/volume7/meinshausen06a/meinshausen06a.pdf
Morales Schechinger, C. (2007). Algunas reflexiones sobre el mercado de suelo urbano. https://es.scribd.com/document/255875677/Algunas-Reflexiones-Sobre-El-Mercado-de-Suelo-Urbano-Carlos-Morales-2007
Porras Garrido, A. (2016). What is the difference between bagging and boosting? QuantDare, Madrid, Spain. https://quantdare.com/what-is-the-difference-between-bagging-and-boosting/
Reese, E. (2003). Instrumentos de gestión urbana, fortalecimiento del rol del municipio y desarrollo con equidad. Lincoln Institute of Land Policy. https://www.academia.edu/1226364/Instrumentos_de_gesti%C3%B3n_urbana_fortalecimiento_del_rol_del_municipio_y_desarrollo_con_equidad
Sabatini, F. (2003). La segregación social del espacio en las ciudades de América Latina. Serie Azul, 35 (2003), 59–70. https://publications.iadb.org/publications/spanish/document/La-segregaci%C3%B3n-social-del-espacio-en-las-ciudades-de-Am%C3%A9rica-Latina.pdf
Smolka, M., & Mullahy, L. (Eds.). (2010). Perspectivas urbanas: Temas críticos en políticas de suelo en América Latina. Lincoln Institute of Land Policy. https://www.lincolninst.edu/sites/default/files/pubfiles/perspectivas-urbanas-cd-full.pdf