Análisis didáctico de una situación: movimiento en dos dimensiones
Pedagogic analysis of a situation: movement in two dimensions
César Cristóbal Escalante1, Verónica Vargas Alejo2 y Martha Leticia García Rodríguez3
1 División de Ciencias e Ingeniería, Universidad de Quintana Roo. Boulevard Bahía e I. Comonfort, Col. del Bosque, CP 98019, Chetumal, Quintana Roo. México.
2 Departamento de Matemáticas, Centro Universitario de Ciencias Exactas e Ingeniería de la Universidad de Guadalajara.México.
3 Departamento de Matemáticas de la Escuela Superior de Ingeniería Mecánica y Eléctrica, IPN. México.
E–mail: cescrist@gmail.com
(Recibido el 12 de mayo de 2017; aceptado el 26 de octubre de 2017)
Resumen
Se describen resultados obtenidos al explorar el potencial didáctico de una actividad. Esta experiencia está inmersa dentro del proceso de elaborar una secuencia didáctica para el tema: Movimiento de Cuerpos en dos dimensiones en un curso de física general a nivel superior. Hacemos énfasis en el análisis de la actividad: Movimiento de un balón de fútbol. Esto nos ayudó a establecer la secuencia que deben seguir los estudiantes al abordar su descripción, y desarrollar los conocimientos conceptuales, y las habilidades considerados en los objetivos del curso. También nos permitió identificar las posibles intervenciones del instructor del curso.
Palabras clave: Análisis Didáctico; Movimiento; Aprendizaje de conceptos.
Abstract
We describe the results obtained by exploring the didactic potential of an activity. We performed this experience by developing a didactic sequence for the theme: Body Movement in two dimensions. We emphasize the analysis of the activity: Movement of a soccer ball. This helped us to establish the sequence students should follow in addressing their description, and to develop the conceptual knowledge and skills considered in the course objectives. It also allowed us to identify the possible interventions of the instructor of the course.
Keywords: Didactic Analysis; Movement; Learning concepts.
La función docente en matemáticas, y en cualquier disciplina, demanda de los profesores diseñar, elaborar o seleccionar, y evaluar las actividades y las formas de trabajo en el aula, que consideran deben realizar los estudiantes para alcanzar los objetivos educativos asociados a cada tema y al curso completo.
Para realizar esta función, los docentes requieren considerar los objetivos educativos e identificar los conocimientos, habilidades y actitudes asociados con la disciplina que están inmersos en ellos y que deben desarrollar los estudiantes; deben identificar los procesos de aprendizaje adecuados y pertinentes por los que deben transitar los alumnos para desarrollar esos conocimientos. En otro nivel de especificidad, los profesores deben elegir o seleccionar el conjunto de actividades, su contenido, el orden, los recursos y las formas de trabajo en el aula de los estudiantes y del instructor, para que los primeros desarrollen los conocimientos asociados con cada tema o unidad. La función docente demanda que los profesores integren conocimientos asociados con la disciplina, con la didáctica de la disciplina, con los procesos de aprendizaje, y sobre los estudiantes (Shulman, 2005).
Para realizar esta integración, los docentes deben dar respuestas a preguntas como las siguientes: ¿Qué hace a una actividad o un conjunto de actividades ser pertinentes para lograr un objetivo específico? ¿Cuáles son los procesos de aprendizaje y cuáles los conocimientos que se deben propiciar con esas actividades? ¿Qué criterios deben utilizarse para seleccionarlas?
Las respuestas que se den a preguntas de este tipo dependen del conocimiento y la comprensión que tenga el docente sobre: la disciplina y sus aplicaciones, el currículoy los objetivos educativos, y las formas en que las personas desarrollan su conocimiento (los procesos de aprendizaje). Los conjuntos de actividades, su contenido, el orden, los recursos y la forma en que son realizadas por los estudiantes, permiten identificar aspectos de los conocimientos y concepciones que él o las personas que las elaboraron tienen sobre la disciplina, los procesos de aprendizaje, y el currículo. En cierto modo, muestran sus concepciones respecto a los conocimientos, habilidades, valores y actitudes que consideran deben aprender los estudiantes y la forma pertinente para aprenderlos (White y Mesa, 2014).
Determinar las actividades, el orden y la forma en que deben ser ejecutadas por los estudiantes para que desarrollen los conocimientos, habilidades y valores señalados en los objetivos educativos, es un proceso continuo y de largo plazo, que requiere de la colaboración y el intercambio entre docentes, expertos en la disciplina e investigadores de los procesos educativos asociados con ella. Las concepciones del docente sobre el proceso de aprendizaje y sobre las matemáticas son fundamentales porque determinan la necesidad de crear uno o distintos escenarios de enseñanza y el tipo de preguntas que pueden apoyar el desarrollo de distintas interpretaciones de la actividad o situación, las cuales evolucionen en complejidad y por lo tanto amplíen el sistema conceptual del estudiante.
Gómez (2002) expone un procedimiento sistemático para analizar un tema o un objetivo educativo concreto del currículo, buscando información útil para sustentar el diseño y la elección de las actividades, de su organización, de las guías para su implementación y para realizar la evaluación, tanto de ellas como de los conocimientos aprendidos por los estudiantes, lo denomina análisis didáctico.
Describimos aquí algunos resultados obtenidos al hacer un análisis didáctico sobre movimiento parabólico y de una actividad asociada con este tipo de movimiento, considerando un sistema de referencia de dos dimensiones. El objetivo fue identificar las características de los conceptos involucrados, sus relaciones y procesos, de manera que, al ser abordadas las actividades en el aula por los estudiantes, se favorezca la comprensión de los conceptos físicos y matemáticos utilizados. Enfatizamos lo correspondiente a la exploración del potencial didáctico de la actividad, esto es, de identificar los conocimientos conceptuales, las habilidades, actitudes y valores que pueden ser desarrollados y refinados con la actividad en el aula.
II. REVISIÓN DE LITERATURA
El proceso de aprendizaje de una persona se realiza cuando interacciona con el medio ambiente en el que se desenvuelve y, en particular en su interacción con otros individuos. En estas interacciones, la persona desarrolla sistemas conceptuales que le permiten explicar, describir, comunicar, pronosticar el comportamiento y evolución de situaciones que se presentan en su ambiente, a otros individuos (o a sí mismo), utilizando sistemas de representación y de comunicación. Estos sistemas conceptuales están constituidos por conceptos (definiciones), relaciones entre conceptos, propiedades de los conceptos y de las relaciones entre ellos. Los sistemas conceptuales construidos por un individuo están en constante transformación, dependiendo de las experiencias desarrolladas en forma individual y colectiva (Lesh y Doerr, 2003).
Las experiencias vividas por un individuo se reflejan en los modelos o sistemas conceptuales (internos) que construye e interioriza en su mente. Para comunicar sus ideas o modelos internos, los individuos construyen modelos externos, utilizando alguna forma de representación.Al hacer lo anterior tienen que adaptar las representaciones propias a representaciones compartidas o consensuadas con otras personas. Durante estos procesos de comunicación se pueden presentar discrepancias entre los modelos internos y externos del individuo, que pueden llevar a cambios en ambos modelos. Cuando las interpretaciones de un modelo externo son compartidas, los modelos internos desarrollados por los individuos pueden ser modificados para acomodarse a las interpretaciones de los otros. En este sentido el aprendizaje es un proceso que implica una serie de ciclos de entendimiento formados por experiencias en las cuales los sistemas conceptuales o modelos van siendo modificados, desde sistemas conceptuales burdos y desarticulados hasta llegar a modelos más refinados e integrados. El proceso de aprendizaje implica construir sistemas conceptuales cuya función es explicar, predecir, comunicar y manipular otros sistemas. Desarrollar la comprensión de un concepto, implica considerarlo en diversas dimensiones: concreto–abstracto, particular–general, en contexto–sin contexto, intuitivo–analítico–axiomático, fragmentado–integrado. El desarrollo de la comprensión de un concepto no se da en forma aislada, sino que está relacionado con la comprensión de otros conceptos asociados (Lesh y Doerr, 2003).
El desarrollo del conocimiento conceptual y el desarrollo de la habilidad de una persona para utilizar ese conocimiento en el análisis de situaciones, o en la resolución de problemas, no se efectúan de forma separada, están estrechamente relacionados (Lesh, 2010). La comprensión de los conceptos se realiza a la par que el desarrollo de la habilidad para utilizarlos en el análisis de situaciones y en la resolución de problemas.
Apoyar el proceso de aprendizaje de los estudiantes que implique el desarrollo, la modificación y la ampliación de su sistema conceptual es una tarea compleja que implica para un docente diseñar, elaborar e implementar actividades o situaciones y evaluarlas.
Simon (1995) utiliza el concepto de trayectoria hipotética de aprendizaje(THA) para referirse a la secuencia de actividades que el profesor o el investigador suponen deben seguir los estudiantes para alcanzar los objetivos de aprendizaje, a partir de las características del conocimiento involucrado.
Gómez (2002) utiliza el concepto de THA al describir el proceso de análisis didáctico, un proceso cíclico útil para que los profesores identifiquen, organicen y evalúen las actividades que lleven a los estudiantes a aprender un contenido específico. Observa que el diseño, la elaboración, la selección, la evaluación de tareas y actividades de enseñanza y aprendizaje que pueden integrar tanto el plan de instrucción de una asignatura, de un tema o de una clase de matemáticas, demandan cuatro tipos de análisis: 1) análisis de contenido, para identificar y organizar los significados de los conceptos y procedimientos involucrados; 2) análisis cognitivo, para describir la trayectoria hipotética de aprendizaje que podrían seguir los estudiantes; 3) análisis de instrucción, para diseñar y elegir las actividades de instrucción pertinentes; y 4) análisis de actuación, para evaluar los conocimientos desarrollados e identificar las dificultades de aprendizaje de los conceptos involucrados.
III. ANÁLISIS DIDÁCTICO DEL MOVIMIENTO DE TIRO PARABÓLICO Y LA SITUACIÓN EL MOVIMIENTO DE UN BALÓN DE FÚTBOL AMERICANO
A. El programa de estudios y la planeación de las clases
La planificación de la instrucción para un curso, unidad, tema o clase requiere realizar los análisis señalados por Gómez (2002), considerando que cada uno presenta dificultades asociadas al carácter global o loca en el contexto curricular.
Mostramos aquí segmentos del proceso y de los resultados al analizar el tema de movimiento en dos dimensiones, de la unidad denominada cinemática, del curso de Física Clásica (ESIME–IPN, 2003) con el propósito de elaborar un plan de instrucción.
Con el propósito de enmarcar la unidad y el tema en el plan global de instrucción del curso, se consideraron los objetivos generales y particulares del curso, cuyos enunciados institucionales son:
Objetivo general: El alumno aplicará algunos conceptos y modelos físico matemáticos básicos de la mecánica newtoniana en el análisis de fenómenos que ocurren en los sistemas físicos, estableciendo las bases de una actitud crítica, racional, científica y analítica. (p. 1)
Objetivos particulares:
El estudiante aplicará los conceptos que involucran los vectores, su formalismo matemático, y su utilidad inmediata en la solución de algunos problemas concretos. (p. 5)
El estudiante aplicará los conceptos de fuerza y torque en sistemas físicos, utilizando algebra vectorial. (p. 6)
El alumno explicará el concepto de cinemática y podrá distinguir entre velocidad media, velocidad instantánea, aceleración media y aceleración instantánea, también analizará las respectivas gráficas de cada una de estas velocidades y aceleraciones. (p. 7)
Es necesario analizar e interpretar estos objetivos, para identificar los objetivos de aprendizaje que guiarán la elección y organización del conjunto de actividades que permitan a los alumnos desarrollar los conocimientos y habilidades involucrados en ello. Esto implica responder preguntas del tipo: ¿Cuáles son los nuevos conceptos que debe desarrollar el estudiante de nivel universitario diferentes a los abordados en el nivel medio superior? ¿Qué nuevos procedimientos debe aprender a utilizar? ¿A partir de qué conceptos se integrarán los nuevos? ¿Cómo se desarrollan los nuevos procedimientos? ¿Cómo deben ser articulados los nuevos conceptos y procedimientos con los previos? ¿Qué problemas y situaciones son pertinentes para que los estudiantes desarrollen esos conocimientos? ¿En qué orden?
De lo anterior se desprendió que los tres objetivos particulares, asociados al objetivo general, demandan que los estudiantes del curso desarrollen conocimientos conceptuales y conocimientos sobre procedimientos asociados conla cinemática y la dinámica. En particular, respecto a cinemática, se considera como objetivos de aprendizaje que los estudiantes desarrollen y refinen conocimientos sobre los conceptos de posición, desplazamiento, velocidad, aceleración, sistema de referencia, vector, representaciones vectoriales y cartesianas, propiedades de los vectores, las componentes de un vector, operaciones con vectores y su representación gráfica en sistemas de representación cartesiano, de manera que puedan ser utilizados para analizar, describir y predecir el movimiento de objetos en dos dimensiones, en particular los denominados tiro vertical, tiro horizontal, tiro parabólico y movimiento circular.
La manera tradicional de abordar estos temas en el aula se basa en un esquema que incluye la definición de los conceptos, seguidos de ejemplos y problemas de aplicación realizados por el instructor del curso, y de ejercicios de tarea para los alumnos. Existen otros caminos para lograrlo.
¿Qué problemas y situaciones son pertinentes para que los estudiantes desarrollen y afirmen esos conocimientos? Dar respuesta a esta pregunta requiere analizar diversas situaciones o problemas que podrían ser utilizadas como actividades que deben realizar los estudiantes, en el aula o fuera de ella, para desarrollar los conocimientos conceptuales, procedimentales, y habilidades establecidos en los objetivos del tema. Requiere valorarlasy organizarlas de acuerdo con las concepciones de lo que es el conocimiento, y de cómo se realiza el proceso de aprendizaje de ese conocimiento. En este caso, utilizamos los que señala la perspectiva de modelos y modelación (Lesh y Doerr, 2003). Al establecer una secuencia de actividades didácticas, es necesario identificar las potencialidades de todas y de cada una de las actividades, para integrarlas, considerando queel conjunto de actividades integrará una secuencia de ciclos de entendimiento o de comprensión donde los estudiantes van enriqueciendo los modelos conceptuales que les permiten explicar las situaciones abordadas. Por ello es importante conocer lo que podría suceder al abordar una actividad particular. Describimos a continuación resultados y el proceso de análisis efectuado a una situación que denominamos “El balón de Fútbol Americano”. Se desea utilizar esta actividad, junto con otras actividades,en una secuencia didáctica para que los estudiantes desarrollaran conocimientos conceptuales y procedimentales asociados con el movimiento en dos dimensiones, de manera que pudieran analizar situaciones semejantes, plantear y responder preguntas, así como resolver problemas asociadas con ellas.
B. Explorando la potencialidad didáctica de una actividad
El balón de Fútbol Americano. El partido de fútbol americano entre los equipos de las Águilas Blancas del IPN y los Cóndores de la UNAM es para determinar el campeón de la temporada. El marcador es 13 a 14 a favor de los Cóndores. Están en los últimos segundos del último cuarto. El partido está por finalizar. Jacinto Licea se encuentra a 40 metros de la portería enemiga, en el centro de la cancha, y patea para un gol de campo. El balón sale con una velocidad inicial de 20 m/s y formando un ángulo de 45° con el suelo.¿Anotará el gol de campo? ¿Ganarán las Águilas Blancas? ¿Con qué ángulo y a qué velocidad debe salir el balón para que Jacinto Licea anote un gol de campo?
Responder las preguntas requiere analizar la situación realizando algunas consideraciones. Una, suponer que el movimiento del balón se realiza en un plano. Otra, que el balón al ser pateado, sale impulsado con una velocidad inicial formando un ángulo θ con el suelo (figura 1).
|
|
|
|
|
|
FIGURA 1. Representación en el plano cartesiano de la salida del balón.
Debe tener información respecto al significado de “gol de campo” en el contexto del fútbol americano y de las dimensiones de la cancha en la que se juega. Esto es:
FIGURA 2. La cancha de fútbol americano tiene las dimensiones que se muestran en la imagen de la derecha. En los extremos al centro se ubica la portería, cuyas dimensiones se proporcionan en la imagen de la izquierda.
Para hacer un gol de campo el balón debe cruzar la región de la portería, denominada Y, que es la región superior de forma rectangular ubicada a 3.05 metros del suelo, con 5.55 metros de largo y con un ancho igual a 3.05 metros (figura 2). La cancha tiene de largo 109.7 m y 48.8 m de ancho, dividida en dos secciones. Debe ubicar la posición desde donde se patea el balón (figura 3)
FIGURA 3. Ubicación del punto de tiro en la cancha de juego.
Los estudiantes deben considerar como se mueve el balón. Ellos deben imaginar y describir ese movimiento. Deben considerar que el balón se mueve desde el suelo, elevándose, hasta llegar a un punto en el que no sube más. Posterior a este momento, la pelota tiende a descender. Durante el movimiento la pelota no solo se eleva, sino que se aleja del punto inicial. Los estudiantes deben elaborar representaciones de este movimiento, hasta derivar en una representación del mismo en un sistema coordenado. En una representación en el plano cartesiano, las diferentes posiciones del balón son puntos en el plano. Cada punto está determinado por las coordenadas (x, y) asociadas a dos direcciones (dimensiones): una horizontal X, la otra vertical Y (figura 4).
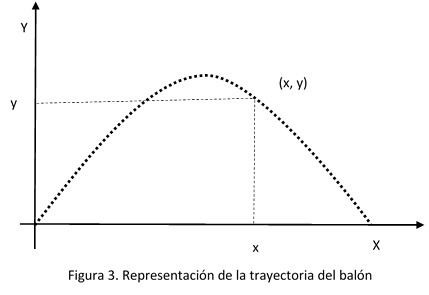
FIGURA 4. Representación de la trayectoria del balón en un sistema de referencia bidimensional.
¿Cómo se determina la posición del balón en cada momento? Para responder esta pregunta, los estudiantes deben asumir que el movimiento del balón es el resultado de dos movimientos simultáneos: uno en la dirección horizontal y otro en la dirección vertical. Es posible que algunos consideren otros factores que inciden en el movimiento, una situación muy compleja que en este momento no se podría abordar. Ello permitiría discutir o analizar una estrategia para simplificar la situación y analizarla suponiendo solamente la incidencia de los dos movimientos señalados.
En la dirección horizontal, el balón sale impulsado por la fuerza aplicada en esa dirección, que le produce una velocidad inicial en esa dirección. Ahora con el objeto de tener una “primera aproximación” en la descripción del movimiento del balón. Se puede asumir que en esta dirección no existe fuerza alguna actuando sobre el balón. Esto es, no existe algo que altere este movimiento. Por ello, se puede decir que el movimiento en la dirección horizontal es un movimiento rectilíneo en el que la velocidad no cambia, se mantiene constante. Este concepto se considera visto en temas anteriores al movimiento en dos dimensiones, por ello, en esta actividad se refuerza su uso y comprensión, así como la estrategia o heurística: Ante un problema complejo buscar aproximarlo por situaciones más simples (Polya, 1973, pp. 30–31).
En la dirección vertical el balón se mueve por el efecto producido por dos fuerzas. Una, que se aplica al golpear el balón, y hace que salga con una velocidad inicial en la dirección vertical, esto es alejándose del suelo. Otra, la fuerza de atracción de la tierra, que lo frena, que lo atrae hacia la tierra. Esta fuerza produce en el balón una desaceleración. Hace que la velocidad inicial con la que sale en la dirección vertical disminuya en el transcurso del tiempo. En la dirección vertical el movimiento del balón, es un movimiento con velocidad variable, es un movimiento uniformemente desacelerado. La velocidad del balón en el movimiento hacia arriba va disminuyendo hasta que se hace cero, y entonces el balón tiende a volver a la tierra. A partir de ese momento, el balón cae.
Lo señalado antes se puede expresar como sigue: la velocidad vo inicial puede verse conformada por dos componentes: una componente horizontal vox y una componente vertical voy(figura 5).Las componentes de vo se obtienen mediante las relaciones:
FIGURA 5. La velocidad inicial y sus componentes en cada dirección.
Como el movimiento en la dirección horizontal, eje X, es un movimiento rectilíneo con velocidad constante, la posición x de la pelota respecto al punto de partida es dada por la expresión:
(1)
El movimiento en la dirección vertical, eje Y, es un movimiento de tiro vertical, en el que el objeto sale con una velocidad inicial v0yy está sujeto a la fuerza de atracción de la tierra, que acelera su movimiento. Por ello la posición y de la pelota respecto al punto de partida es dada por la expresión:
(2)
La posición del balón está dada por los puntos (x, y) tales que:
(3)
Estas expresiones permiten ubicar la posición del balón en el tiempo y el espacio. El estudiante debe percatarse de que la información proporcionada coincide con la posición esperada. Esto demandará al estudiante evaluar diferentes situaciones del balón. Al hacerlo el estudiante podría tomar comprensión de la situación y de la expresión para identificar la posición. El profesor podría impulsar a los estudiantes a considerar diferentes momentos, esto es a dar valores al tiempo, desde que se golpea el balón y analizar su posición en cada instante, esto es a explorar y analizar la información proporcionada por la relación (3).Después de esta exploración, el profesor puede hacer preguntas como las siguientes: Considerando el punto de salida como centro de referencia. ¿En qué posición se encuentra el balón un segundo después de salir?
La respuesta a esta pregunta implica responder lo siguiente: ¿Qué distancia horizontal ha recorrido en un segundo? ¿Qué distancia vertical ha recorrido en un segundo? E integrándolas en la respuesta a la pregunta: ¿Cuál es la posición un segundo después respecto al punto de salida?
La siguiente situación permite buscar que el estudiante reafirme y busque generalizar el proceso para dar respuesta a preguntas análogas donde se cambia el tiempo:
Considerando el punto de salida como centro de referencia. ¿En qué posición se encuentra el balón dos segundos después de salir? ¿Qué distancia horizontal ha recorrido? ¿Qué distancia vertical ha recorrido? ¿Cuál es la posición respecto al punto de salida?
Considerando el punto de salida como centro de referencia. ¿En qué posición se encuentra el balón 5 segundos después de salir?
Considerando el punto de salida como centro de referencia. ¿En qué posición se encuentra el balón 10 segundos después de salir?
Responder estas preguntas permite al estudiante desarrollar su comprensión de la necesidad de un sistema de referencia para ubicar la posición del balón, e iniciar la construcción de la trayectoria del balón utilizando las diferentes posiciones. Al calcular y observar las posiciones del balón, el estudiante confronta las conjeturas y supuestos iniciales.
En este momento, se puede integrar el uso de la hoja de cálculo para ampliar el número de posiciones de la trayectoria, en menor tiempo. Esto puede contribuir a desarrollar en los estudiantes la capacidad de uso de la hoja de cálculo como una herramienta (figura 5).
Preguntas como la siguiente permiten al estudiante explorar el efecto del ángulo de salida. El profesor debe plantear preguntas pertinentes o inducir a los estudiantes a proponer y responderlas. Ejemplos:
La pelota es pateada, sale con una velocidad de 20 m/s y haciendo un ángulo de 45° con el suelo. ¿Se anota un gol de campo?
¿En qué posición se encuentra el balón cuando está sobre la línea de gol?
FIGURA 6. Procedimiento en Excel para realizar los cálculos.
Esta pregunta puede ser respondida a partir de la tabla (figura 6). Donde se observa que no será un gol de campo.
Se pueden hacer variaciones al problema, que lleven a los estudiantes a considerar la situación desde otras perspectivas. Por ejemplo, cambiando la velocidad de salida y manteniendo el ángulo de salida respecto del suelo:
Si la pelota es pateada y sale con una velocidad de 22 m/s, haciendo un ángulo de 45° con el suelo. ¿Se anota un gol de campo?
Si la pelota es pateada y sale con una velocidad de 20 m/s, haciendo un ángulo de 60° con el suelo. ¿Se anota un gol de campo?
Si la pelota es pateada y sale con una velocidad de 20 m/s, haciendo un ángulo de 35° con el suelo. ¿Se anota un gol de campo?
Esto lleva a utilizar el procedimiento elaborado en Excel modificando la velocidad y el ángulo, obteniendo nueva información y observando el potencial de la hoja de cálculo para realizarlos (figura 6 y 7).
Plantear una variante de esta situación, permite llevar al estudiante a explorar el uso de la hoja de cálculo desde otra perspectiva: Si la pelota es pateada y sale haciendo un ángulo de 45° con el suelo. ¿Con que velocidad debe salir para que se anote un gol de campo?
FIGURA 7. Explorando el ángulo de salida.
Aquí se pide al estudiante explore o determine la velocidad usando el procedimiento en Excel (figura 8).Este contexto, también permite que los estudiantes se acerquen y den significado a conceptos como las cantidades vectoriales (en relación con las cantidades escalares). La posición y la velocidad del objeto requieren ser ubicadas en el sistema de referencia, indicando su dirección y su magnitud. ¿Qué representa la magnitud de cada uno? En este punto es importante la distinción entre desplazamiento y recorrido.Así, el cambio de posición se asocia con el desplazamiento, y es un vector. El recorrido es asociado con las diferentes posiciones del objeto. En este sentido, la situación que aquí se discute, permite distinguir entre ambos conceptos.Medir el recorrido del balón implica determinar la longitud de la trayectoria seguida.
El estudiante puede observar que después de recorrer 40 metros horizontalmente el balón debe tener una altura igual o mayor que 3.05 metros. Al cambiar la velocidad de salida en el procedimiento (hoja electrónica), la respuesta será aproximada.
También puede responder usando las expresiones (1) y (2), haciendo la suposición de que la altura debe ser mayor o igual que 3.05 metros cuando la distancia recorrida es 40 metros, esto es, debe suponer que la posición es (40, 3.05), por ejemplo, y resolver el sistema de ecuaciones:
FIGURA 8. Usando Excel para explorar variaciones en la velocidad y en el ángulo de salida.
Las condiciones iniciales de la situación pueden ser modificadas, se pueden plantear preguntas sobre las variables características de la situación.Esto lleva a considerar un conjunto de problemas anidados en un mismo contexto. Al resolverlos el estudiante irá construyendo la idea del modelo, como un recurso que permite explicar, predecir, comunicar, describir una situación.
IV. REFLEXIONES FINALES
El análisis de la actividad exhibe la estrecha vinculación entre los conocimientos físicos y matemáticos, como sistema de referencia, vector, leyes del movimiento, velocidad, aceleración, posición, representaciones vectoriales y cartesianas, propiedades de los vectores, las componentes de un vector, operaciones con vectores y su representación gráfica en sistemas de representación cartesiano. Estos conceptos son los elementos del sistema conceptual asociado al movimiento de tiro parabólico. La relación entre estos conceptos no puede ser separada en los procesos de desarrollo del conocimiento y de las capacidades intelectuales de los estudiantes.
El proceso de análisis de la situación permite al profesor identificar los procesos de razonamiento que deben seguir los estudiantes para comprender la situación, para establecer las relaciones con los conocimientos previamente aprendidos, para robustecerlos y para identificar nuevos conceptos, así como su utilidad para describir las situaciones, para explicar aspectos de la misma, para predecir lo que sucederá o no, para realizar estimaciones e interpretarlas.
Los resultados obtenidos en el análisis de la situación o problema permiten identificar algunas de sus potencialidades didácticas, de las cuales puede derivarse alguna forma en que puede ser presentada a los estudiantes en el aula, así como las formas de intervención del profesor para guiar y enfatizar el trabajo de los estudiantes hacia los objetivos establecidos para el tema. Los resultados pueden sugerir la necesidad de incluir herramientas tecnológicas (hoja de cálculo) para realizar operaciones, agilizar los procesos de análisis y desarrollar la comprensión de los conceptos físicos y matemáticos, como los sistemas de referencia, sistemas de coordenadas, modelos, cantidades vectoriales, y de las habilidades para plantear y valorar conjeturas asociadas con variaciones de la situación. Permite también identificar características que deben tener otras actividades para complementar el proceso de aprendizaje de los conceptos involucrados.
REFERENCIAS
ESIME–IPN (2003). Programa del curso Física Clásica de ICA. http://www.esimez.ipn.mx/OfertaEducativa/Documents/ingenieria_en_control_y_automatizacion/pe_1er_semetre/02–FISICA_CLASICA.pdfSitio consultado el 16 de octubre de 2012.
Gómez, P. (2002).Análisis didáctico y diseño curricular en matemáticas. Revista EMA, 7(3), 251–292. http://funes.uniandes.edu.co/1537/ Sitio consultado el 26 de junio de 2015
Lesh, R. (2010). Tools, Researchable Issues & Conjectures for investigating what it means to understand Statistics (or other topics) meaningfully. Journal of Mathematical Modeling and Application, 1(2), 16–48.
Lesh, R. y Doerr, H. M. (2003). Foundations of a Models and Modeling perspective on mathematics teaching, learning, and problem solving. En Richard Lesh y Helen M. Doerr (Eds.) (2003). Beyond Constructivism. Models and modeling perspectives on mathematics problem solving, learning, and teaching . Mahwah, NJ: Lawrence ErlbaumAssociates, pp.3–35.
Polya, G. (1989). Cómo plantear y resolver problemas. México: Trillas.
Shulman, L. S. (2005).Conocimiento y enseñanza: Fundamentos de la nueva reforma. Profesorado. Revista de currículum y formación del profesorado, 9(2), 1–30 https://www.ugr.es/~recfpro/rev92ART1.pdfSitio consultado el 17 de enero de 2007.
Simon, M.A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26, 114–145.
White, N. y Mesa, V. (2014). Describing cognitive orientation of Calculus I tasks across different types of coursework. ZDM Mathematics Education 46, 675–690. DOI 10.1007/s11858–014–0588–9. https://link.springer.com/journal/11858/46/4/page/1 Sitio consultado el 12 de enero de 2014.