LA SECUENCIA DE FIBONACCI Y LOS MECANISMOS DE EFICIENCIA ENERGETICA: HACIA UN USO RACIONAL Y EFICIENTE DE LA ENERGIA A NIVEL MACROSCOPICO
MAXIMILIANO F. CAMARDA
Comisión de Eficiencia Energética del Comité de Energías Córdoba (CEC)
Centro de Investigaciones y Estudios sobre Cultura y Sociedad (CIECS) – (CONICET- UNC). Córdoba, Argentina.
maxi_camarda@hotmail.com
Fecha recepción: junio 2021 Fecha aprobación: octubre 2021
ARK CAICYT: http://id.caicyt.gov.ar/ark:/s18539777/lpf2vaduw
RESUMEN
Las emisiones exacerbadas de carbono atmosférico, producto de más de un siglo de actividades antropogénicas, han permitido, a la humanidad y a las diversas especies del planeta, navegar sin brújula en un gran océano de crisis climática.
El desarrollo de nuevos paradigmas científicos, la consolidación de nuevos sistemas de gobernanza climática y la implementación de novedosos sistemas de gestión de la energía, es una necesidad tan trascendente como prioritaria para los Estados soberanos de todos los continentes.
En este trabajo, se presenta una breve reseña de los descubrimientos científicos de las últimas décadas que han incorporado la secuencia numérica de Fibonacci a nivel microscópico, con importantes resultados a nivel tecnológico, energético y ambiental.
En este sentido, si la energía, así como un gran número de elementos del universo, poseen una estructura de comportamiento compatible con los números F, se debería comenzar a hablar de conceptos como la dimensión espacio-tiempo-energética de Fibonacci.
El diseño de mecanismos de eficiencia energética basado en la secuencia de Fibonacci constituye un desafío a escala macroscópica que permitiría mejorar la gestión de los recursos energéticos, económicos y naturales, colaborando con la reducción de la intensidad energética y las emisiones de carbono atmosférico.
PALABRAS CLAVES: Serie de Fibonacci - Proporción Áurea - Elasticidad Áurea-Energética - Eficiencia Energética - Elasticidad de la Intensidad Energética - Desarrollo Económico Sostenible
ABSTRACT
The exacerbated emissions of atmospheric carbon, product of more than a century of anthropogenic activities, have allowed humanity and several other species in the planet to navigate aimlessly in a huge ocean of climate crisis.
The development of new scientific paradigms, the consolidation of new climate governance systems and the implementation of innovative energy management systems is not only a significant need but also a priority for sovereign States on all continents.
In this work, a brief review is presented of the scientific discoveries of the last decades that have incorporated the Fibonacci number sequence at the microscopic level, with important results at the technological, energy and environmental level.
In this sense, if energy, as many other elements on the universe, has a behavioral structure compatible with the F numbers, we should start talking about concepts such as the Fibonacci space-time-energy dimension.
The design of energy efficiency mechanisms based on the Fibonacci sequence constitutes a challenge on a macroscopic scale that would allow improving energy, economic and natural resources management, thus cooperating with the reduction of energy intensity and atmospheric carbon emissions.
KEYWORDS: Fibonacci Sequence - Golden Ratio - Energy Ratio Elasticity - Energy Efficiency - Energy Intensity Elasticity - Sustainable Economic Development
1. INTRODUCCION
El avance inminente del cambio climático genera graves problemas en el medio ambiente, la economía y la salud humana. Los Estados soberanos a nivel mundial deberán tomar decisiones cruciales sobre cómo gestionar la energía, los recursos naturales, las ciudades, los efectos migratorios, la salud, las actividades antropogénicas, etc., si pretenden dar cumplimiento a los Objetivos de Desarrollo Sostenible 2030 y al Acuerdo de París (CEPAL, 2018).
Encontrar respuestas concretas a la amplia diversidad de problemas y necesidades existentes, exige de la creación de nuevos modelos y paradigmas mentales sobre el rol de los Estados modernos, el desarrollo de la ciencia, el buen uso de la tecnología y la relación entre el ser humano y el Planeta en que habita.
El desarrollo de nuevos paradigmas científicos en el campo de la energía nos invita a despertar consciencia sobre la importancia del uso racional y eficiente de la energía, a repensar la concepción sobre los usos y aplicaciones energéticas y los medios o dispositivos tecnológicos que el ser humano necesita para satisfacer su sistema de preferencias energéticas.
Repensar el uso de la tecnología destinada a ahorrar energía, conduce a explorar nuevos mundos, tanto a nivel microscópico como macroscópico; lleva a indagar y preguntarse cómo funciona el planeta en un universo infinito determinado por ciertas estructuras y a descubrir cómo los avances científicos en aplicaciones tecnológicas pueden colaborar con el desarrollo de un consumo energético más eficiente y responsable.
En este sentido, el estudio de la secuencia numérica de Fibonacci representa una oportunidad para conocer una estructura de comportamiento matemática que posee la capacidad suficiente para explicar diversos fenómenos y elementos del universo. Dicho ordenamiento matemático, a través de los años, pudo observarse en la reproducción de algunos animales, en la disposición de semillas en algunas plantas, en los pétalos de una flor, en las relaciones entre las ramas y hojas de los árboles, en la formación de planetas, huracanes, ondas en el agua, entre otros.
Si el sistema funcional y orgánico de diversas especies arbóreas tiene como objetivo ahorrar agua y energía solar para realizar el proceso de fotosíntesis, pues entonces, se puede afirmar que existe un diseño natural que permite la reproducción, la supervivencia de las especies y la continuidad de la vida orgánica.
A un nivel muy pequeño, microscópico, se observaron relaciones basadas en los números F entre protones, electrones, longitudes de enlace, etc. Un importante descubrimiento son los denominados cuasicristales y el desarrollo de nuevos materiales y tecnologías con diversas aplicaciones en los mercados de bienes y servicios en general, y en los mercados de bienes y servicios de la eficiencia energética y energías renovables en especial.
El diseño de mecanismos de un programa de eficiencia energética (PEE) basado en la serie de Fibonacci, invita a reconciliar los aspectos microscópicos y macroscópicos; es un llamado a recomprender la estructura y funcionalidad de los elementos del universo, desde aspectos tan sutiles como las partículas elementales hasta la manipulación de dispositivos tecnológicos por los consumidores/usuarios de la energía.
Desde esta perspectiva, toda política energética que pretenda reducir la intensidad energética y el nivel de emisiones de carbono atmosférico deberá trabajar a nivel microscópico (en el mundo de lo pequeño) y a nivel macroscópico (en el mundo de lo grande), con la universalidad de actores existentes (Gómez, Sella Piedrabuena y Mathé, 2013; Navarro Gómez, 2017; OLADE, 2017, 2019).
2. LA SECUENCIA NUMERICA DE FIBONACCI Y EL NUMERO AUREO
Según el trabajo de Stakhov (2007), la Teoría de los Números de Fibonacci o Números F y la “sección de oro o dorada”, constituyen una de las ramas más importantes de las matemáticas modernas.
La serie se inicia con el valor “1”, por lo tanto, el primer número de la serie F1꞊ 1, el término siguiente Fn+1, es decir F2, se obtiene a través de la suma de los dos valores anteriores y también es igual a 1. En este sentido, se puede expresar a los números F de la siguiente manera (1) (Stakhov, 2014):
![]() (1)
(1)
La secuencia queda conformada por los siguientes números:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
Aquellas sucesiones como la descrita anteriormente, donde todo término se determina en función de los anteriores, se denominan sucesiones recurrentes y son muy frecuentes en el campo de las matemáticas (Vorobiov, 1974).
La sucesión (1) con F1 ꞊ F2 ꞊ 1 se denomina Sucesión de Fibonacci y cada uno de sus términos se denominan números de Fibonacci (números F).
Además, si realizamos el cociente entre dos números consecutivos de la serie (2), dicho resultado converge a un valor denominado Número Áureo o Proporción Áurea (Φ).
![]()
(2)
El número Φ es aproximadamente igual a 1,618…, se trata de un número irracional similar al número Pi (π). La proporción dada por Φ es conocida desde la antigüedad como la sección dorada o proporción divina (Ghyka, 1978a, 1978b,1979).
Para valores muy grandes de la variable, cuando n tiende a infinito, obtenemos la siguiente expresión (3):
![]()
(3)
El resultado de la expresión (3), constituye el valor al que tiende el número Φ, para dimensiones espacio-tiempo muy distantes.
En la publicación de 1855, “Aestetische Forschungen”, realizada por el alemán Zeising, se expresa lo siguiente: “para que un todo, dividido en partes desiguales, parezca hermoso desde el punto de vista de la forma, debe haber entre la parte menor y la mayor la misma razón que entre la mayor y el todo” (Ghyka, 1979: 38).
En nuestro caso, si por ejemplo se toma el consumo total de energía de un país dado por el segmento (CTE), y se realiza una doble partición en base al uso racional y eficiente de energía, se obtienen dos subsegmentos conformados por el consumo eficiente de energía (CEE) y el consumo ineficiente de energía (CIE), que nos permitirían identificar el consumo energético dorado (CED) (FIGURA 1).

FIGURA 1: Consumo Energético Dorado o Proporción Energética Divina. Fuente: Elaboración propia.
En el contexto de la eficiencia energética, la proporción energética divina (4), se encontraría asociada a una razón entre dos proporciones que oscilan entre el uso eficiente y racional de la energía y la ineficiencia en la gestión de los recursos energéticos.
La proporción energética divina, podríamos expresarla de la siguiente manera:
![]()
(4)
El Consumo Energético Dorado (CED), representa un estadio de bienestar óptimo en el proceso de asignación de recursos energéticos, tanto en el desarrollo de opciones de fuentes como usos y aplicaciones energéticas.
La proporción energética divina, implica una situación de equilibrio natural y armónica entre los mercados energéticos, los mercados de bienes y servicios y las riquezas naturales de un país, en lo que respecta al consumo de energía. Aquellos países que pretendan afrontar un proceso de transición energética justo y equitativo, deberán implementar políticas tendientes a redireccionar los diferentes perfiles de consumo energético a través de una hoja de ruta de la eficiencia energética.
La transición energética, implica avanzar continuamente a través de múltiples equilibrios de Nash eficientes (Camarda, 2018), buscando la combinación ideal de diferentes consumos energéticos que minimicen las pérdidas energéticas y las emisiones de carbono, hasta encontrar un equilibrio energético estable, al que se podría denominar Óptimo Energético de Fibonacci (OEF).
3. APLICACIONES DE LA SECUENCIA DE FIBONACCI EN EL CAMPO DE LA ENERGIA
Si bien se puede encontrar la sucesión de Fibonacci en diferentes disciplinas científicas, inicialmente gran parte de la comunidad académica demostró un gran nivel de escepticismo al respecto. No obstante, hacia finales del siglo XX la concepción de los físicos teóricos respecto a los números F y la proporción de oro cambió radicalmente. Algunos trabajos como los de Shechtman, Mauldin y William, El Naschie, Vladimirov, entre otros, han demostrado que los progresos en el campo de la física y la cosmología se encuentran asociados a la relación de oro (Stakhov, 2007).
Según Bleher (1990), en el campo de la mecánica cuántica, a un nivel de escala muy pequeño, el número Φ se observa en la relación de frecuencias de un par de osciladores armónicos. En física nuclear, el radio de Bohr del Hidrógeno demostró ser la suma de dos secciones de oro pertenecientes al electrón y al protón; a su vez, las longitudes de enlace entre dos átomos representan la suma de dos secciones de oro de los radios del anión y el catión (Heyrovska, 2013a, 2013b).
Otros trabajos basados en datos experimentales de longitudes de onda de líneas espectrales de hidrógeno para evaluar la constante de Rydberg, la constante de estructura fina y el factor de relatividad de Sommerfeld, demuestran su relación con la proporción de oro (Heyrovska, 2013c). Además, en Sherbon (2018) se puede encontrar la relación dorada en el cálculo de constantes de estructura fina, así como en la relación masa protón-electrón.
En magnetismo, algunas investigaciones demuestran la presencia de la razón dorada en materiales magnéticos compuestos, ya que en una colección de partículas de estados ligados la masa es reducida. Según Figueroa, Castro, Fox y Lozano (2013), determinar la razón de las masas desde un análisis relativista es un problema más complejo.
Una alternativa que se presenta es mediante la aplicación de métodos de teoría cuántica de campos. En este sentido, Coldea et al. (2010), trabajando experimentalmente con el material “cobalto de niobato”, describe la existencia de la proporción dorada en una razón de masas de dos cuasipartículas de baja energía. Estos resultados se relacionan a las estructuras denominadas E8 (hidden), dentro de los Grupos de Lie.
Por otra parte, en Figueroa et al. (2013) puede observarse la aplicación de los Números F al análisis de circuitos eléctricos de infinitas resistencias en serie y en paralelo. Además, se realiza un análisis del problema aerodinámico de Newton para conos truncados en base a Cruz Sampedro y Tetlalmatzi Montiel (2010), demostrando que el cono de mínima resistencia es aquel que se construye con proporciones áureas (Stakhov, 2005).
Otros trabajos de aplicaciones generalizadas de Fibonacci, sobre el cálculo de corrientes y voltajes nodales a circuitos tipo escalera y el voltaje a lo largo de una línea de transmisión continua, mediante técnicas de formalismo matricial que incluyen el cálculo de eigenvalores, la diagonalización y la potenciación de matrices 2x2, pueden observarse en Sanjinés Castedo (2010).
En el campo de las matemáticas, las funciones hiperbólicas de Fibonacci y Lucas constituyen uno de los descubrimientos matemáticos modernos más trascendentes, con gran influencia en la física teórica y en la comprensión de las leyes que gobiernan las estructuras que forman el Universo. En este sentido, en paralelo con el espacio hiperbólico basado en funciones hiperbólicas clásicas, encontramos el espacio hiperbólico de oro basado en las funciones hiperbólicas de Fibonacci y Lucas (Stakhov, 2011).
4. Opciones de Eficiencia Energética a escala Microscópica: Desarrollo de Nanoestructuras a través de los Números F
El surgimiento de nuevas tecnologías y el creciente interés en descubrir nuevos materiales con propiedades físicas específicas, ha generado avances significativos en el campo de las Nanoestructuras (Hutchison, 2016).
Según González Zacarías, Palomino Ovando y Cocoletzi (2010), la utilización de técnicas de crecimiento epitaxial de nano-heteroestructuras para fabricar sistemas multicapas periódicas y aperiódicas posee numerosas aplicaciones en la industria optoelectrónica. En la última década existió un gran interés en estudiar la propagación de la radiación electromagnética en estructuras fotónicas por su trascendencia en múltiples aplicaciones industriales.
Por ejemplo, una de las propiedades físicas más importantes que se investigan en los cristales fotónicos, es la estructura de bandas, que describe el rango de frecuencias en que a la luz se le permite o prohíbe propagarse a través del cristal. En el primer caso hablamos de bandas y en el segundo de brechas; la aparición de bandas y brechas para la propagación de ondas electromagnéticas es una consecuencia de la periodicidad de la estructura.
Dicha propiedad puede utilizarse en la fabricación de filtros destinados a la propagación direccional de la luz (Ghulinyan, Oton, Dal Negro, Pavesi, Sapienza, Colocci y Wiersma, 2005).
Por otra parte, pueden diseñarse estructuras cuasi-periódicas a través de la secuencia que poseen los números de Fibonacci con resultados interesantes (González Zacarías, Palomino Ovando y Cocoletzi, 2010; Merlin, Bajema, Clarke, Juang y Bhattacharya, 1985).
En diversos campos de aplicación que posee la eficiencia energética, la pregunta que debería hacerse es la siguiente: cuál es la estructura que permite una propagación más eficiente de la luz a los efectos de multiplicar los beneficios asociados a esa distribución secuencial, en cuanto a productividad, grado de calidad e impacto ambiental.
Numerosos trabajos confirman el hecho de que las Nanociencias pueden contribuir a descubrir tecnologías más eficientes y respetuosas con el medio ambiente, a través del aporte de opciones más racionales en cuanto a generación, almacenamiento, transporte, distribución y consumo de energía.
En cuanto a las aplicaciones en los mercados energéticos, las nanotecnologías constituyen una herramienta extremadamente útil y versátil, que puede mejorar el perfil de eficiencia de los materiales fotovoltaicos utilizados en dispositivos de energía solar, mediante la integración de nanoestructuras de nuevos y más sofisticados materiales (Ferry, Atwater y Polman, 2011). Los avances en el diseño de células solares fotovoltaicas permiten combinar un gran rendimiento de captación y conversión de los fotones solares en energía eléctrica, con un diseño inteligente y el empleo de materiales abundantes que favorecen las economías de escala.
Las consecuencias de estas aplicaciones tecnológicas pueden observarse en un mayor grado de productividad de los paneles solares, una mejor gestión en el proceso de captación y almacenamiento de la energía solar, una mayor reducción del consumo de energía eléctrica provenientes de recursos no renovables, y un menor nivel de emisiones de carbono (Pala, Liu, Barnard, Askarov, Garnett, Fun y Brongersma, 2013).
En relación con el almacenamiento de energía, estas tecnologías permiten disponer de baterías ligeras, potentes, económicas, fiables y reciclables; por ejemplo, con diversas aplicaciones en el campo de la movilidad eléctrica.
Otras aplicaciones industriales y de servicios, puede lograrse gracias al descubrimiento de los cuasicristales (Landauro, 2011; Bindi, Steinhardt, Yao y Lu, 2009). Éstos, son estructuras que, dadas sus propiedades físicas y estructurales como su bajo coeficiente de fricción, elevada dureza, baja energía superficial y resistencia al desgaste, poseen un gran potencial de aplicaciones tecnológicas. El rediseño a nivel de nanoestructuras de materiales como el aluminio, permitiría mejorar su grado de calidad transformándolo en un material más ligero y liviano, aumentando su vida útil. Esto permitiría reducir el consumo energético de este tipo de materiales, que es utilizado en prácticamente todos los sectores industriales.
Además, los nuevos materiales desarrollados a través de nanotecnologías poseen una doble ventaja en torno a la eficiencia energética; por un lado, poseen la capacidad de generar el mínimo consumo energético en el proceso de manipulación para producir otros bienes y servicios, y, por otro lado, permiten obtener bienes y servicios más sofisticados con eficiencia energética más elevada. Para un análisis de los requerimientos energéticos en el proceso de desarrollo de nanotecnologías, puede observarse Ferreira (2010).
4.1. Nanofotónica y Plasmónicos
La nanofotónica es un área emergente y multidisciplinaria enfocada en la innovación en campos tales como, celdas solares, sistemas luminiscentes eficientes para pantallas o iluminación de bajo consumo energético, sistemas de señalización lumínica persistente, etc. (Yang, Jiasen y Lian-Mao, 2018).
Durante décadas, la eficiencia de las células solares ha tenido un rendimiento inferior respecto a los límites termodinámicos, no obstante, los nuevos enfoques respecto a la gestión de la luz permitirán obtener parámetros de ultra elevada eficiencia (Atwater y Polman, 2012). Por lo tanto, se puede afirmar que existe una nueva tendencia de investigaciones con el propósito de mejorar el rendimiento de las células solares de película delgada (Atwater y Polman, 2010). Los Plasmónicos (o plasmonics), constituyen un espacio de investigación respecto a esta materia.
La nanofotónica y los plasmónicos, constituyen disciplinas científicas que trabajan en “el mundo de lo pequeño”, y generan grandes repercusiones en “el mundo de lo grande”, lo que permite desarrollar nuevas tecnologías destinadas a promover el uso racional y eficiente de la energía.
El potencial de aplicación diversificado que posee es muy elevado, desde sectores industrializados energointensivos con tecnología predominante, hasta sectores de consumo masivo con tecnología simple. Los sectores beneficiarios de estas tecnologías son los siguientes: energéticos; biomedicina; telecomunicaciones; navegación terrestre, marítima, aérea, aeroespacial; informática; seguridad; automotriz; alimentación; indumentaria; electrodomésticos; tecnológicos (por ej. domótica), entre otros.
Las ventajas de las nanotecnologías permiten ahorrar energía eléctrica en equipos electrónicos (PCs, módems, routers, tablets, TV, radios, etc.), reducir el tamaño de los dispositivos, y aumentar las velocidades de operación y transmisión de datos (transmisiones de Gbit/s).
Desde el punto de vista de la eficiencia energética se puede reducir el consumo de energía eléctrica gracias a la posibilidad de sustitución total de chips electrónicos por chips fotónicos, o bien parcial, logrando la combinación de componentes electrónicos y fotónicos en un mismo chip, a través de los plasmónicos (Ozbay, 2006). En telecomunicaciones e informática (Williams, 2004), un uso más eficiente de los dispositivos tecnológicos permite acceder a información en forma más rápida y segura, y reducir el tiempo de utilización de los equipos para lograr satisfacer la misma necesidad, sin alterar el nivel de confort en la prestación del servicio (Ali et al., 2015).
Según Giannini, Fernández-Dominguez, Heck y Maier (2011), la creación de nanoantenas permite redirigir la energía electromagnética que se propaga en el espacio, en modos localizados de dimensiones inferiores a la longitud de onda de la radiación; una de las ventajas, es que estas nanoantenas poseen mayor eficiencia energética respecto a las metálicas.
Nuevos nanodiseños en el campo de la automoción, robótica y domótica, pueden colaborar con la programación de máquinas y tecnologías que permitan un uso más eficiente y responsable de los recursos en las plantas industriales. Esta ventaja permite reducir el despilfarro de insumos, los tiempos en los procesos productivos y de distribución, y, en consecuencia, el consumo energético en cada eslabón de la cadena de valor (Camarda, 2020; Zhao, Liu, He, Cao y Guo, 2017).
En el campo de la electrónica, la posibilidad de producir equipos más eficientes colabora con un uso racional de la energía, fundamentalmente en sectores de consumo masivo donde la demanda agregada de productos y energía es elevada (Murphy, Kenig, Allen, Laurent y Dyer, 2003).
4.2. Aplicaciones Tecnológicas e Informáticas
Según los trabajos de Stakhov (1980, 2014, 2015), la teoría de números dorados y las nuevas propiedades que se presentan en los números naturales (Z-propiedad, D-propiedad, Φ-código, F-código y L-código), también poseen gran repercusión en el desarrollo del sector informático y las telecomunicaciones. Las Matemáticas de la Armonía, constituyen una fuente de inspiración para el desarrollo de nuevas tecnologías de información, como la Tecnología de Información Dorada basada en los códigos p de Fibonacci y los códigos de las proporciones p doradas.
El fin principal de los sistemas numéricos posicionales dorados y de Fibonacci, es consolidar las matemáticas, la informática y la metrología digital en un enfoque íntegro y completo (Stakhov, 2016). Esta conjunción permitiría desarrollar sistemas de computación y medición con un elevado grado de confiabilidad en nanoestructuras, aplicables a un gran número de sectores industriales y de servicios, como los mercados de bienes y servicios de la eficiencia energética y las energías renovables.
5. los numeros F, el numero aureo y el consumo energetico
En las dos secciones siguientes, definimos la relación entre el consumo de energía (CE) y el nivel de actividad económica (PIB), a los efectos de determinar un indicador clave denominado elasticidad de la intensidad energética (EIE). Luego, comparamos la tasa de crecimiento de la IE con la tasa de crecimiento áureo de un determinado recurso con patrones F. Supongamos, el crecimiento de las semillas de girasol, soja o maíz y su relación con el CE en el proceso de elaboración de biocombustibles tales como, biodiesel, bioalcoholes (bioetanol, biometanol, biobutanol), biogás, gas de síntesis, y biocombustibles sólidos (madera, carbón vegetal y aserrín); la estructura de la molécula de agua y su función en represas hidroeléctricas.
5.1. Cálculo de la Elasticidad de la Intensidad Energética
La elasticidad de la intensidad energética (EIE), mide el grado de sensibilidad en las variaciones del consumo energético (CE) ante cambios en el nivel de actividad económica (PIB), en una determinada dimensión espacio-tiempo de Fibonacci Di (Ei-Ti-Fi). Este indicador (5), permite identificar el grado de variación porcentual en el CE por cada 1% en que varía el PIB.
![]()
(5)
Para cambios infinitesimales en las variables, la elasticidad adquiere la siguiente forma (6):
![]()
(6)
Donde ![]() representa la
pendiente de la función de elasticidad de la intensidad energética (FIGURA 2).
representa la
pendiente de la función de elasticidad de la intensidad energética (FIGURA 2).
De acuerdo con la naturaleza y estructura de la producción agregada, las fuentes energéticas, y los diferentes perfiles de consumo energético predominantes, pueden presentarse tres alternativas:
1. ![]() : En este caso,
la variación porcentual en el CE en di es inferior a la
variación porcentual en el PIB, ello implica, que por cada 1 % en que varía la
producción agregada, las variaciones porcentuales en el consumo de energía son
inferiores al 1 %. La elasticidad entre las variables es “inelástica”, y el grado
de eficiencia energética es elevado, ya que las políticas de gestión energética
permiten desacoplar el consumo de energía respecto al nivel de actividad
(gráficamente a partir de D2).
: En este caso,
la variación porcentual en el CE en di es inferior a la
variación porcentual en el PIB, ello implica, que por cada 1 % en que varía la
producción agregada, las variaciones porcentuales en el consumo de energía son
inferiores al 1 %. La elasticidad entre las variables es “inelástica”, y el grado
de eficiencia energética es elevado, ya que las políticas de gestión energética
permiten desacoplar el consumo de energía respecto al nivel de actividad
(gráficamente a partir de D2).
2. ![]() : La variación
porcentual en el CE en di es igual a la variación
porcentual en el PIB, es decir, por cada 1 % en que varía la producción
agregada, las variaciones porcentuales en el consumo de energía son iguales al
1 %. La elasticidad entre las variables es “unitaria”, y el grado de eficiencia
energética es de carácter neutral (obsérvese el punto D2).
: La variación
porcentual en el CE en di es igual a la variación
porcentual en el PIB, es decir, por cada 1 % en que varía la producción
agregada, las variaciones porcentuales en el consumo de energía son iguales al
1 %. La elasticidad entre las variables es “unitaria”, y el grado de eficiencia
energética es de carácter neutral (obsérvese el punto D2).
3. ![]() : Esta
situación se presenta cuando la variación porcentual en el CE en di
es mayor a la variación porcentual en el PIB. Por cada 1 % en que varía la
producción agregada, las variaciones porcentuales en el consumo de energía son
superiores al 1 %. La elasticidad entre las variables es “elástica”, y el grado
de eficiencia energética es reducido (gráficamente entre D0 y D2).
: Esta
situación se presenta cuando la variación porcentual en el CE en di
es mayor a la variación porcentual en el PIB. Por cada 1 % en que varía la
producción agregada, las variaciones porcentuales en el consumo de energía son
superiores al 1 %. La elasticidad entre las variables es “elástica”, y el grado
de eficiencia energética es reducido (gráficamente entre D0 y D2).
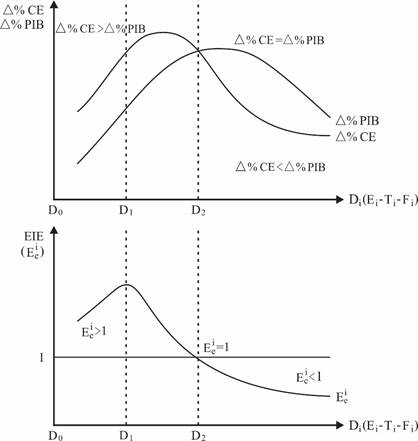
FIGURA 2: Delimitación de la Elasticidad de la Intensidad Energética (EIE). Fuente: Elaboración propia.
5.2. Cálculo y Bondades de la Elasticidad Aurea-Energética
La Elasticidad Aurea-Energética (EAE), es un indicador que mide el grado de sensibilidad con que reacciona la intensidad energética (o el consumo energético), ante cambios en el crecimiento áureo (CA) de diferentes recursos o eventos naturales, en una determinada dimensión espacio-tiempo de Fibonacci Di (Ei-Ti-Fi) (7).
Este indicador posee varias ventajas, la más trascendente es su capacidad para analizar el grado de eficiencia energética en la gestión de recursos naturales, energéticos y tecnológicos asociados a distintos sectores industriales, etapas de procesamiento, niveles de actividad, ciclos económicos, ciclos de vida de productos/servicios, etc.
Desde esta perspectiva, la EAE se constituye como un instrumento capaz de evaluar la efectividad de determinadas políticas y programas públicos y/o privados, basados en la preservación de recursos naturales y el uso racional y eficiente de la energía.
Se puede definir matemáticamente de la siguiente manera:

(7)
Donde:
![]() ꞊
Elasticidad Aurea-Energética del recurso “j” en la dimensión espacio
tiempo de Fibonacci Di (Ei-Ti -Fi).
꞊
Elasticidad Aurea-Energética del recurso “j” en la dimensión espacio
tiempo de Fibonacci Di (Ei-Ti -Fi).
![]() ꞊ Tasa
de crecimiento de la intensidad energética asociada al recurso “j” en la
dimensión espacio tiempo de Fibonacci Di (Ei-Ti -Fi).
꞊ Tasa
de crecimiento de la intensidad energética asociada al recurso “j” en la
dimensión espacio tiempo de Fibonacci Di (Ei-Ti -Fi).
![]() ꞊ Tasa
de crecimiento áurea del recurso “j” en la dimensión espacio tiempo de
Fibonacci Di (Ei-Ti -Fi).
꞊ Tasa
de crecimiento áurea del recurso “j” en la dimensión espacio tiempo de
Fibonacci Di (Ei-Ti -Fi).
Las oscilaciones de la intensidad energética respecto al crecimiento natural de los recursos, da origen a distintas situaciones:
1. ![]() : En este caso,
las variaciones de la IE en di son superiores a las variaciones en
el CA; la capacidad predictiva del indicador advierte una situación donde el
perfil de consumo energético asociado a un sector, actividad o proceso está
consumiendo más energía respecto a la tasa natural de crecimiento o
reproducción de dicho recurso. Esta situación manifiesta la presencia de un conjunto
de patrones de consumo energético de carácter ineficientes.
: En este caso,
las variaciones de la IE en di son superiores a las variaciones en
el CA; la capacidad predictiva del indicador advierte una situación donde el
perfil de consumo energético asociado a un sector, actividad o proceso está
consumiendo más energía respecto a la tasa natural de crecimiento o
reproducción de dicho recurso. Esta situación manifiesta la presencia de un conjunto
de patrones de consumo energético de carácter ineficientes.
2. ![]() : Las
variaciones de la IE en di son idénticas a las variaciones en el CA,
razón por lo cual, se identifica un comportamiento del consumo energético
similar al crecimiento áureo, dando origen a patrones de consumo energético de
carácter normales o áureos.
: Las
variaciones de la IE en di son idénticas a las variaciones en el CA,
razón por lo cual, se identifica un comportamiento del consumo energético
similar al crecimiento áureo, dando origen a patrones de consumo energético de
carácter normales o áureos.
3. ![]() : Aquí, el
consumo de energía por unidad de valor agregado en di se encuentra
por debajo de los niveles de crecimiento áureos, identificando una estructura
de patrones de consumo energético de carácter eficientes.
: Aquí, el
consumo de energía por unidad de valor agregado en di se encuentra
por debajo de los niveles de crecimiento áureos, identificando una estructura
de patrones de consumo energético de carácter eficientes.
La ![]() brinda
información valiosa para poder analizar, evaluar, y cuantificar la brecha
existente en materia de eficiencia energética y emisiones de gases de efecto
invernadero (GEI), en torno a los procesos normales de desarrollo biológico de
determinados recursos naturales y sectores.
brinda
información valiosa para poder analizar, evaluar, y cuantificar la brecha
existente en materia de eficiencia energética y emisiones de gases de efecto
invernadero (GEI), en torno a los procesos normales de desarrollo biológico de
determinados recursos naturales y sectores.
Desde esta perspectiva, su utilidad reside en la capacidad para generar políticas públicas preventivas y/o correctivas en todas aquellas actividades primarias, secundarias o terciarias, inherentes a determinados sectores o procesos que se alejan de las buenas prácticas en el uso racional y eficiente de la energía y generan un mayor nivel de emisiones de carbono atmosférico.
6. LOS SISTEMAS DE GESTION DE LA ENERGIA Y LAS ESTRUCTURAS F
Las estructuras de comportamiento de los consumidores/usuarios de la energía se puede observar a través de los diferentes perfiles de consumo energético, lo que da origen a una cierta fisonomía de la TCIE. De manera similar, las estructuras de comportamiento y/o reproducción natural de determinados recursos y elementos se representan a través de la fisonomía de la TCA.
Si comparamos la TCA con la TCIE (FIGURA 3), se puede determinar el nivel socialmente deseado de consumo de energía y emisiones de GEI, respecto a recursos que manifiestan un comportamiento áureo, identificando el Umbral Dorado de Eficiencia Energética y Sustentabilidad (UDEES).
El UDEES, representa un equilibrio de formación estable, tanto desde el punto de vista económico, como energético, ambiental y social. Se encuentra integrado por un consumo energético dorado (CED) y un nivel de emisiones dorado de GEI (NEDGEI).
6.1. Etapas de un Sistema de Gestión Energética de Fibonacci
El análisis del umbral permite diferenciar y clasificar el análisis de la gestión de los recursos energéticos en diversas etapas, a las que se pueden denominar, Etapas de la Gestión Energética de Fibonacci (EGEF).
Se puede dividir el proceso de gestión en tres fases:
1. Etapa I: Entre D0 y D’1, la TCIE avanza a tasa creciente hasta el punto de inflexión de la curva, donde continúa su recorrido a tasa decreciente hasta llegar a un máximo al finalizar la etapa I. La EAE > 1, crece hasta llegar a un máximo en el punto de inflexión, luego continúa su fase descendente a partir de D’1. Las emisiones de carbono crecen hasta llegar a un máximo, cuando el consumo energético por unidad de valor agregado llega a su mayor valor en D1 (fin de la etapa I e inicio de la etapa II).
2. Etapa II: En una situación ideal, la TCIE es decreciente y la TCA es levemente creciente durante toda la etapa II, lo que se refleja en un nivel de emisiones de carbono con una tendencia decreciente, aunque la EAE > 1.
El comienzo de la etapa II
constituye una situación clave, ya que las decisiones implementadas pueden
tomar rumbos distintos con consecuencias opuestas sobre la economía, la
sociedad y el ambiente. Una política de crecimiento económico basada en el
despilfarro de los recursos energéticos solo generaría una tendencia creciente
de la intensidad energética ![]() la elasticidad áurea
la elasticidad áurea ![]() y el
nivel de emisiones de carbono
y el
nivel de emisiones de carbono ![]() , ampliando continua y sostenidamente la
Brecha de Eficiencia Energética y la Brecha de Emisiones de Carbono
Atmosférico, entre una situación ideal y una situación claramente perjudicial.
, ampliando continua y sostenidamente la
Brecha de Eficiencia Energética y la Brecha de Emisiones de Carbono
Atmosférico, entre una situación ideal y una situación claramente perjudicial.
El punto máximo de la curva TCIE, constituye un punto crítico (para una sociedad en D1), entre la continuidad de un modelo de crecimiento basado en la ineficiencia económica y el derroche energético y un proceso de transición energética caracterizado por la eficiencia económica y energética. A este punto lo denominamos Punto de Bifurcación Energética (PBE).

FIGURA 3: Relaciones entre la Elasticidad Áurea Energética y las Emisiones de Gases de Efecto Invernadero. Fuente: Elaboración propia.
3. Etapa III: Al final de la etapa II e inicio de la etapa III, en D2, la TCIE logra acoplarse al ritmo y cauce natural de la TCA, razón por lo cual la elasticidad áurea energética es unitaria (EAE = 1). A partir de D2, la TCIE < TCA y la EAE < 1. El nivel de emisiones de GEI continúa su fase decreciente, logrando niveles históricamente no alcanzados desde D0.
6.2. Beneficios de un Sistema de Gestión Energética de Fibonacci y el Análisis del Umbral de Eficiencia Energética y Sustentabilidad
En el UDEES se verifica un proceso de convergencia entre las estructuras de comportamiento áureas o doradas correspondientes a los diversos elementos de la naturaleza y las estructuras de comportamiento antropogénicas.
Las políticas de eficiencia energética implementadas, en especial a partir de D1, permitirían inferir que el consumo energético por unidad de valor agregado en D2 se encuentra en plena sintonía con los niveles de crecimiento natural de los recursos.
El cálculo del umbral podría realizarse a nivel macroeconómico, o bien a nivel microeconómico. A nivel micro, sería conveniente indagar en la relación del consumo energético respecto a un recurso o grupo de recursos conforme a cada actividad industrial, proceso de producción/prestación de servicios, ciclo de vida de un sector industrial, empresa o producto/servicio.
Para cualquier Di ≠ D2, podríamos determinar las políticas de gestión energéticas necesarias para lograr que la economía en su conjunto, sector industrial u organización económica, tienda a ubicarse en una situación de equilibrio económico, energético, ambiental y social.
Las políticas y mecanismos de eficiencia energética implementados en un proceso de transición energética, que tienen como meta alcanzar el UDEES permitirían obtener múltiples beneficios, tales como, reducir el consumo energético, los costes energéticos, y las emisiones de carbono, además de generar retornos económicos. Por otro lado, este tipo de mecanismos basados en la secuencia de Fibonacci conducirían a salvaguardar la reproducción de especies vegetales, animales, minerales, etc. a través de un consumo energético responsable que respeta la evolución natural de dichas especies. En definitiva, estas medidas garantizarían una aproximación hacia niveles óptimos de explotación de recursos naturales, eliminando riesgos económicos, energéticos, ambientales y sociales producto de niveles elevados de sobreexplotación.
7. CONCLUSIONES
La secuencia de Fibonacci representa una serie numérica capaz de demostrar una estructura matemática que puede observarse en los vastos elementos del universo, el campo de la energía es uno de ellos.
Las numerosas aplicaciones científicas y tecnológicas en el campo de la energía demuestran claramente la presencia de una geometría universal en elementos de carácter microscópicos. En este sentido, los avances realizados en el campo de las nanoestructuras ofrecen una oportunidad trascendente en el desarrollo de equipos, productos y tecnologías más eficientes, que permiten ahorrar energía y mejorar el nivel de confort de los consumidores y usuarios. Las nanotecnologías generan grandes beneficios, tanto en los segmentos de oferta como de demanda de energía.
A nivel macroscópico, todavía es necesario seguir indagando en el desarrollo de nuevos mecanismos de eficiencia energética que permitan encontrar un umbral de equilibrio económico, energético, ambiental y social.
En este sentido, la elasticidad áurea-energética y el análisis UDEES, permiten incorporar a la secuencia de Fibonacci en el estudio de los mecanismos de eficiencia energética. Este tipo de análisis brinda la posibilidad de detectar anomalías energéticas y ambientales en torno al uso de determinados recursos naturales y fuentes energéticas, corrigiendo y redireccionando los diferentes perfiles de consumo energético hacia prácticas basadas en el uso racional y eficiente de la energía.
Este tema requiere especial atención en aquellos sectores energointensivos, que utilizan recursos naturales en distintos eslabones de la cadena de valor con una estructura de comportamiento compatible con la secuencia de Fibonacci.
El rediseño de estructuras de comportamiento en los diferentes perfiles de consumo energético, hacia estructuras de comportamiento que se encuentran en la naturaleza y el universo, permitiría encontrar oportunidades que no sólo conducen a reducir el consumo energético y las emisiones de carbono, sino también a controlar y preservar la supervivencia de determinados recursos naturales garantizando una sostenibilidad eficiente a largo plazo.
8. REFERENCIAS
Ali, M. et al. (2015). Energy-Efficient Abundant-Data Computing: The N3XT 1,000x. Computer, 48(12), 24-33.
Atwater, H. y Polman, A. (2010). Plasmonics for improved photovoltaic devices. Nature Materials, 9, 205-213.
Atwater, H. y Polman, A. (2012). Photonic design principles for ultrahigh-efficiency photovoltaics. Nature Materials, 11, 174-177.
Bindi, L., Steinhardt, P., Yao, N. y Lu, P. (2009). Natural Quasicrystals. Science, 324(5932), 1306-1309.
Bleher, P. M. (1990). The Energy Level Spacing for Two Harmonic Oscillators with Golden Mean Ratio of Frequencies. Journal of Statistical Physics, 61 (3-4), 869-876.
Camarda, M. F. (2018). Teoría de Juegos en el campo de la Eficiencia Energética: Análisis de la dinámica Industrial en la búsqueda de un equilibrio de Nash eficiente. Revista EPIO, 26(44), 41-60.
Camarda, M. F. (2020). Just-in-Time y Eficiencia Energética. Implicancias en los Sistemas de Gestión de la Energía y Procesos de Descarbonización de Sistemas Industriales. Revista EPIO, 28(48), 58-77.
Coldea, R. et al. (2010). Quantum criticality in an-Ising Chain: Experimental evidence for Emergent E8 symmetry. Environmental Science & Technology, 36(24), 5504-5510.
Comisión Económica para América Latina y el Caribe (CEPAL) (2018). Segundo informe anual sobre el progreso y los desafíos regionales de la Agenda 2030 para el Desarrollo Sostenible en América Latina y el Caribe, Santiago de Chile, 2018, 1-181.
Cruz Sampedro, J. y Tetlalmatzi Montiel, M. (2010). POEM’s and Newton´s Aerodynamic Frustrum. The College Mathematics Journal, 41(2),145-153.
Ferreira, P. (2010). Requerimientos de Energía en los Procesos de Fabricación a Nanoescala. Lámpsakos, 4, 36-43.
Ferry, V., Atwater, H. y Polman, A. (2011). Modeling Light Trapping in Nanostructured Solar Cells. ACS Nano, 5(12), 10055-10064.
Figueroa, C., Castro, L., Fox, J. y Lozano, M. (2013). La Secuencia de Fibonacci y el Número de Oro en Ingeniería Eléctrica y Análisis Numérico. Revista Formación Universitaria, Centro de Información Tecnológica (CIT), La Serena, Chile, 6(2), 23-32.
Giannini, V., Fernández-Dominguez, A., Heck, S. y Maier, S. (2011). Plasmonics Nanoantennas: Fundamentals and their use in controlling the radiative properties of nanoemitters. Chemical Reviews, 111(6), 3888-3912.
Ghulinyan, M., Oton, C., Dal Negro, L., Pavesi, L., Sapienza, R., Colocci, M. y Wiersma, D. (2005). Light-pulse propagation in Fibonacci quasicrystals. Physical Review B, 71(9).
Ghyka, M. (1978a). El Número de Oro, Tomo I los Ritmos, Editorial Poseidón.
Ghyka, M. (1978b). El Número de Oro, Tomo II los Ritos, Editorial Poseidón.
Ghyka, M. (1979). Estética de las Proporcionas en la Naturaleza y en las Artes, Editorial Poseidón.
Gómez, G., Sella Piedrabuena, L. y Mathé, L. (2013). “Eficiencia Energética”. En Matriz de recursos energéticos de la Provincia de Córdoba, Devalis S. (Ed.), Editorial Copiar, Córdoba, República Argentina, 95-129.
González Zacarías, C., Palomino Ovando, M. A. y Cocoletzi, G. H. (2010). Los números de Fibonacci en la naturaleza y los sistemas nanoestructurados artificiales. Revista Interdisciplinaria en Nanociencias y Nanotecnologías, Universidad Nacional Autónoma de México, 3(1), 15-28.
Heyrovska, R. (2013a). Atomic and Ionic Radii of Elements and Bohr Radii from Ionization Potentials are Linked Through the Golden Ratio. International Journal of Sciences, vol. 2, marzo 2013.
Heyrovska, R. (2013b). Atomic, Ionic and Bohr Radii Linked via the Golden Ratio for Elements of Groups 1 - 8 including Lanthanides and Actinides. International Journal of Sciences, vol. 2, abril 2013.
Heyrovska, R. (2013c). Golden Ratio Based Fine Structure Constant and Rydberg Constant for Hydrogen Spectra. International Journal of Sciences, vol. 2, mayo 2013.
Hutchison, J. (2016). The road to sustainable nanotechnology: challenges, progress, and opportunities. ACS Sustainable Chemistry & Engineering, 4(11), 5907-5914.
Landauro, C. (2011). Los cristales aperiódicos: treinta años del descubrimiento de los cuasicristales. Revista de Química PUCP, 25(1-2), 34-37.
Merlin, R., Bajema, K., Clarke, R., Juang, F. y Bhattacharya, P. K. (1985). Quasiperiodic GaAs-AlAs heterostructures. Physical Reviews Letters, 55(17), 1768-1770.
Murphy, C., Kenig, G., Allen, D., Laurent, J-P. y Dyer, D. (2003). Development of parametric material, energy, and emission inventories for wafer fabrication in the semiconductor industry. Environmental Science & Technology, 37(23), 5373-5382.
Navarro Gómez, J. (2017). Propuesta metodológica para la elaboración de planes nacionales de eficiencia energética para los países del Sistema de la Integración Centroamericana. Comisión Económica para América Latina y el Caribe (CEPAL), febrero 2017, 1-105.
Organización Latinoamericana de Energía (OLADE) (2017). Eficiencia Energética en América Latina y el Caribe: Avances y Oportunidades, diciembre 2017, 1-82.
Organización Latinoamericana de Energía (OLADE) (2019). Infraestructura de la Calidad para Programas de Eficiencia Energética en América Latina y el Caribe, mayo 2019, 1-99.
Ozbay, E. (2006). Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions. Science, 311, 189-193.
Pala, R., Liu, J., Barnard, E., Askarov, D., Garnett, E., Fun, S. y Brongersma, M. (2013). Optimization of non-periodic plasmonic light-trapping layers for thin-film solar cells. Nature Communications, 4, 2095, 1-7.
Sanjinés Castedo, D. (2010). Sucesión generalizada de Fibonacci aplicada a circuitos tipo escalera. Revista Boliviana de Física,17, 41-46.
Sherbon, M. (2018). Fine-Structure Constant from Golden Ratio Geometry. International Journal of Mathematics and Physical Sciences Research, 5(2), 89-100.
Stakhov, A. (1980). The “Golden Ratio” in Digital Technology. Automation and Computer Engineering, 1, 27-33.
Stakhov, A. (2005). The Generalized Principle of the Golden Section and its applications in mathematics, science, and engineering. Chaos, Solitons & Fractals, 26(2), 263-289.
Stakhov, A. (2007). The Generalized Golden Proportions, a New Theory of Real Numbers, and Ternary Mirror-Symmetrical Arithmetic. Chaos, Solitons & Fractals, 33(2), 315-334.
Stakhov, A. (2011). Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar´s Geometry, and Gilbert´s Fourth Problem. Applied Mathematics, 2, 181-188.
Stakhov, A. (2014). A History, the Main Mathematical Results and Applications for the Mathematics of Harmony. Applied Mathematics, 5, 363-386.
Stakhov, A. (2015). The “Golden” Number Theory and New Properties of Natural Numbers. British Journal of Mathematics & Computer Science, 11(6), 1-15.
Stakhov, A. (2016). Fibonacci p-codes and Codes of the “Golden” p-proportions: New Informational and Arithmetical Foundations of Computer Science and Digital Metrology for Mission-Critical Applications. British Journal of Mathematics & Computer Science, 17(1), 1-49.
Vorobiov, N. N. (1974). Números de Fibonacci. En Carlos Vega (Trad.), Editorial MIR, Moscú.
Williams, E. (2004). Energy intensity of computer manufacturing: Hybrid assessment combining process and economic input-output methods. Science, 327(5962), 177-180.
Yang, L., Jiasen, Z. y Lian-Mao, P. (2018). Three-dimensional integration of plasmonics and nanoelectronics. Nature Electronics, 1, 644-651.
Zhao, G., Liu, Z., He, Y., Cao, H. y Guo, Y. (2017). Energy consumption in machining: Classification, prediction, and reduction strategy. Energy, 133, 142-157.