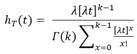MODELO DE DENSIDAD PARA UN ÍNDICE DE EXPOSICIÓN A PLAGUICIDAS APLICADO EN TRABAJADORES RURALES
OLGA E. PADRÓ1 - MARÍA I. STIMOLO1,2 - MARÍA D. P. DÍAZ3,4
1Facultad de Ciencias Económicas - Universidad Nacional de Córdoba. Córdoba, Argentina.
2Centro de investigación en Ciencias Económicas - CIECS (CONICET-UNC). Córdoba, Argentina.
3Instituto de Investigaciones en Ciencias de la Salud - INICSA (CONICET-UNC). Córdoba, Argentina.
4Facultad de Ciencias Médicas - Universidad Nacional de Córdoba. Córdoba, Argentina.
olga.padro@unc.edu.ar-maria.ines.stimolo@unc.edu.ar-pdiaz@fcm.unc.edu.ar
Fecha recepción: junio 2021 Fecha aprobación: octubre 2021
ARK CAICYT: http://id.caicyt.gov.ar/ark:/s18539777/abueifk1q
RESUMEN
Dado que la agricultura es una de las principales actividades productivas de la provincia de Córdoba (Argentina), es importante el estudio del uso de los plaguicidas y su efecto en la salud de los trabajadores rurales. En particular, los agroaplicadores cuya salud está más expuesta al riesgo de uso de los plaguicidas. En este sentido el Grupo de Epidemiología Ambiental del Cáncer en Córdoba, Facultad de Ciencias Médicas, UNC (GEACC) definió un índice del Nivel de Intensidad a la Exposición (IE), de los plaguicidas para medir el riesgo de exposición de los agroaplicadores de la provincia de Córdoba.
A partir de una muestra de trabajadores rurales, se buscó una distribución adecuada para el índice, se tuvieron en cuenta los modelos de las variables de vida desde los más tradicionales (exponencial, Weibull, lognormal, gamma, Birnbaum-Saunders y Gaussiana inversa) hasta las nuevas distribuciones (Birnbaum-Saunders Generalizada e Inversa Gaussiana Tipo). En este trabajo, el mejor ajuste para el IE se logró con la distribución Weibull. A partir del ajuste definido se estimaron los percentiles y se delimitaron tres niveles de riesgo (bajo, medio y alto). En función a estos niveles de riesgo se estudiaron características sociodemográficas y de salud de los trabajadores dentro de cada grupo. Los factores que resultaron más significativos para determinar el riesgo de los aplicadores fueron: la antigüedad (mayor a 10 años) en las tareas de mezclar, aplicar o estar presente mientras se manipulan plaguicidas, no tener receta de ingeniero agrónomo, inyectar animales y la presencia de signos de irritación.
PALABRAS CLAVE: Exposición de plaguicidas – Bondad de ajuste –Distribución de variables de vida- Birnbaum-Saunders Generalizada – Inversa Gaussiana Tipo
ABSTRACT
Since agriculture is one of the main productive activities in Córdoba province, Argentina, it is necessary that special attention be paid to the use of pesticides and their effect on the health of agro-applicators. One way to measure the consequences of the application of this type of substances is through the Index Level of Intensity at Exposure (IE), built by the Group of Environmental Epidemiology of Cancer in Córdoba, Faculty of Medical Sciences, UNC (GEACC), for the population of rural workers in Córdoba.
From a sample of rural workers, the empirical characteristics of the index were analyzed to infer about its population distribution. In the search for an adequate distribution for the intensity index, the models of the life variables were taken into account from the most traditional (exponential, Weibull, lognormal, gamma, Birnbaum-Saunders and inverse Gaussian) to the new distributions (Generalized Birnbaum-Saunders and Inverse Gaussian Type). In this work, the best fit for IE was achieved with the Weibull distribution. Once the best fit was defined, the percentiles were estimated, and three risk levels were defined (low, medium, and high). Based on these risk levels, sociodemographic and health characteristics of the workers within each group were studied. The following factors resulted the most significant to determine the risk of the applicators: the seniority (greater than 10 years) in the tasks of mixing, to apply or be present while it is handling pesticides, not to have an agronomist prescription, to inject animals and to present signs of irritation.
KEYWORDS: Pesticide exposure - Goodness of fit - Life variables distribution- Generalized Birnbaum-Saunders - Inverse Gaussian Generalized
1. INTRODUCCIÓN
El estudio de los plaguicidas, y su impacto en la salud de los trabajadores rurales, adquirió importancia en los últimos años debido al aumento de la superficie cultivada con un sistema de producción que tiene incorporado el uso de los mismos. Particularmente, en la provincia de Córdoba, entre 1996 y 2018, se duplicó la superficie sembrada de los cuatro cultivos principales (girasol, maíz, trigo y soja), con un incremento del 109,67% (Dirección de Estimaciones Agrícolas - Dirección Nacional de Agricultura, 2018).
Conjuntamente con el aumento de superficie sembrada, los nuevos sistemas de producción incorporan el uso de agroquímicos; por lo que los trabajadores rurales se encuentran aún más expuestos a los efectos negativos de sus componentes tóxicos. Surge la necesidad de encontrar una herramienta que permita valorar o medir, de alguna manera, el riesgo a la exposición que experimenta un trabajador rural que está en contacto con este tipo de tóxicos cotidianamente. El origen de esta preocupación está en los efectos adversos que los agentes químicos tienen sobre la salud. Por lo tanto, el riesgo es potencial y no una posibilidad real, es decir, se puede evaluar estadísticamente. (Vilca et al., 2010). Medir el riesgo por la exposición a plaguicidas en un individuo o en una población determinada es complejo, pues está influenciado por factores como la diversidad de productos comercializados, su uso indiscriminado, la multiplicidad de las fuentes de exposición y la variación en la intensidad y la duración de la exposición en un lapso de tiempo.
A partir de diferentes criterios se construyeron indicadores de riesgo a la exposición a plaguicidas como el de Dosemeci et al. (2002) que, a partir del estudio prospectivo de 58.000 aplicadores de Carolina del Norte y Iowa, explica como desarrollaron dos algoritmos para identificar distintos escenarios de exposición de los aplicadores.
El Grupo de Epidemiología Ambiental del Cáncer en Córdoba de la Facultad de Ciencias Médicas de la Universidad Nacional de Córdoba (GEACC[1]) construyó el índice Nivel de Intensidad a la Exposición (IE) aplicado a la población de trabajadores rurales de Córdoba a partir de una adaptación del índice provisto por Docemesi et al., en 2002 (Lantieri et al., 2011).
Estudios preliminares del índice IE[2], evaluado en un conjunto de trabajadores rurales, reportó empíricamente una distribución asimétrica a la derecha, con alta frecuencia de valores atípicos, de soporte positivo.
Estas características empíricas sugieren que este índice se distribuye como una variable de vida. Las variables de vida son continuas, asumen valores positivos y, si bien en general representan el tiempo de vida de un organismo biológico, la duración de un componente electrónico o el tiempo de espera hasta que un sistema falle (Marshal & Olkin, 2007); también pueden tener otras aplicaciones como medir la concentración de un contaminante (Leiva et al., 2010), siendo esta última aplicación de especial interés para el estudio del IE.
Una distribución de vida (life distribution) es un modelo de probabilidad asociado con una variable de vida (Marshal & Olkin, 2007). Una distribución de vida es, en general, asimétrica, unimodal y sesgada positivamente; suele tener dos parámetros al menos y poseer momentos de cualquier orden. Tradicionalmente se utilizaron, para este tipo de variables aleatorias, las distribuciones: exponencial, Weibull, lognormal, gamma, Birnbaum-Saunders y la Gaussiana inversa. Los modelos de tiempo de vida arriba citados se ajustan razonablemente bien a los datos en la parte central de la distribución, pero poseen desempeños pobres en las colas de las mismas. Ajustar las colas de la distribución se convierte en un aspecto muy importante en el análisis debido a, por ejemplo, los problemas de garantía (dosis letales) y mantenimiento (emergencias ambientales), que a menudo se encuentran en los percentiles altos o bajos de la distribución.
Por lo tanto, se torna necesario considerar modelos de vida con mayor flexibilidad, como los modelos BSG (Birnbaum-Saunders Generalizada) y los modelos IGT (Inversa Gaussiana Tipo) (Leiva et.al., 2008).
En este trabajo se estudia el comportamiento del índice Nivel de Intensidad a la Exposición (IE) evaluado en una muestra de 2.209 aplicadores terrestres de la provincia de Córdoba. Así, se analiza la distribución empírica del mismo y se propone un modelo de probabilidad que describa adecuadamente estas características. Se comienza estudiando las distribuciones tradicionales para variables de vida: exponencial, gamma, lognormal, Weibull, Inversa Gaussiana y Birnbaum-Saunders. Luego, se consideran los modelos que debieran ser plausibles, en función de sus fundamentos teóricos y sus propiedades, como los empleados con éxito para analizar datos relacionados con la acumulación de algún tipo de daño o los utilizados por ejemplo para la valoración de la concentración de contaminantes ambiental, es decir, los modelos: BSG (Birnbaum-Saunders Generalizada) y los modelos IGT (Inversa Gaussiana Tipo). En la Tabla 12 se resume las características principales de los modelos utilizados en el ajuste distribucional del índice.
La selección de la distribución candidata se valida mediante el análisis del comportamiento de la tasa de riesgo, empleando el gráfico TTT (Total Time On Test). Una vez elegido el modelo de probabilidad que presente el ajuste más satisfactorio, se estiman los percentiles poblacionales que determinan los niveles de baja, media y alta exposición a plaguicidas. Un análisis descriptivo de los percentiles calculados permite caracterizar estos grupos en función de características sociodemográficas y de la salud de los trabajadores.
2. ÍNDICE DE EXPOSICIÓN A PLAGUICIDAS
En este trabajo se toma en cuenta el índice Nivel de Intensidad a la Exposición (IE) elaborado por el GEACC, basado en la versión construida por Docemesi et al., en 2002 (Lantieri et al., 2011).
2.1 Población de estudio
La información fue recolectada por investigadores del GEACC a partir de una encuesta autoadministrada entregada a 2.209 agroaplicadores de la provincia de Córdoba. El instrumento utilizado es una adaptación, también llevada a cabo por el GEACC, del cuestionario AHS (Bonner & Alavanja, 2005) y consta de cinco módulos, los cuales recogen datos demográficos, características sobre el uso de plaguicidas, información sobre cultivos, variables relacionadas con los hábitos de vida y la salud del trabajador y su familia.
2.2 Construcción del Índice Nivel de Intensidad a la Exposición
El índice de exposición tiene en cuenta lo siguiente: si el trabajador mezcla plaguicidas, si los aplica, los métodos de aplicación que utiliza, si realiza tareas como rociar o sumergir animales, tratamiento de semillas o reparación de maquinarias, la distancia (en metros) de la vivienda al cultivo más cercano y un indicador de protección personal de los trabajadores que tiene en cuenta el equipo de protección utilizado; elaborado también por el GEACC[3].
A partir de los indicadores y las ponderaciones establecidas se calculó un índice de Nivel de Intensidad a la Exposición (IE), según la expresión:
![]()
donde, Mez representa el puntaje de mezcla, EPP el score de nivel de protección, Met el score de cada método de aplicación utilizado por el trabajador, Cant la cantidad de métodos de aplicación utilizados por cada trabajador, Repara es una variable indicadora para señalar a los que reparan maquinarias y DV es el score para la distancia de la vivienda al cultivo más cercano.
Este índice es una combinación lineal de variables cuantitativas y cualitativas, lo que implica que no resulta sencillo el ajuste estadístico de la distribución que lo representa.
3. APLICACIÓN A TRABAJADORES RURALES DE LA PROVINCIA DE CÓRDOBA
Para estudiar el comportamiento de la distribución del IE se consideró en primer lugar las distribuciones de variables de vida tradicionales: exponencial, Weibull, lognormal, gamma, Birnbaum-Saunders y Gaussiana inversa. Y luego, aquellas introducidas como generalizaciones, los modelos BSG (Birnbaum-Saunders Generalizado) y los modelos IGT (Inversa Gaussiana Tipo), que resultan más flexibles para ajustar las colas de la distribución[4].
3.1 Selección del modelo de ajuste
Los pasos que se siguieron para el ajuste de la distribución son:
1. Ajuste gráfico de la distribución empírica del índice a las distribuciones de vida mencionadas.
2. Análisis del desempeño del ajuste a través de criterios de información.
3. Validación de la distribución elegida con los gráficos TTT (Total Time On Test).
3.1.1 Análisis Gráfico
El ajuste gráfico de la distribución empírica del índice con las distribuciones de vida mencionadas en el punto anterior se muestra en la FIGURA 1. Dentro de la figura se presentan (a) el histograma de la distribución empírica del Índice de Intensidad con los ajustes de las distribuciones y (c) la función acumulada o de distribución empírica del Índice de Intensidad y de las distribuciones teóricas; que se complementan con los gráficos (b) Q-Q plot, que representa los cuantiles teóricos versus los cuantiles empíricos, y (d) P-P plot, el cual representa las probabilidades teóricas versus las probabilidades empíricas. El Q-Q plot muestra la falta de ajuste en las colas de la distribución, mientras que el P-P plot enfatiza la falta de ajuste en el centro de la distribución.
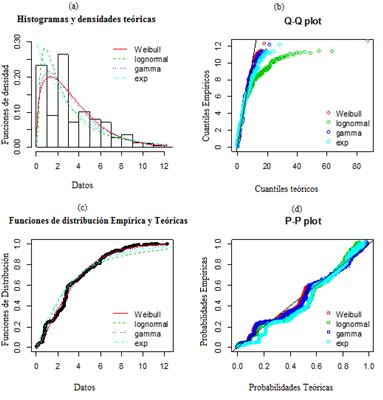
FIGURA 1: Análisis Gráfico de los datos del Índice de Intensidad versus distribuciones tradicionales.
Fuente: Elaborados con el paquete de lenguaje R “fitdistrplus”.
Se observa así que ninguna de las cuatro distribuciones propuestas ajusta correctamente el centro de la distribución de los datos, no obstante, se prefirieron las distribuciones Weibull y Gamma por su mejor descripción de la cola derecha de la distribución empírica; especialmente, porque esta tendencia hacia la derecha es relevante en el contexto de evaluación de riesgos.
El análisis gráfico anterior se realizó también con las nuevas distribuciones (Barros et al., 2008) y se concluyó que ninguna de las BSG ni de las IGT resultaron en ajustes satisfactorios para las distribuciones empíricas de los datos.
3.1.2 Criterios de Información
En una segunda etapa se analizaron los ajustes utilizando los criterios de información: de Akaike (AIC), el Bayesiano de Schwarz (BIC) y el de Hannan-Quinn (HQIC) para todas las distribuciones, tanto para las tradicionales (Exponencial, Lognormal, Weibull, Inversa Gaussiana, Birnbaum-Saunders, Gamma) como para las nuevas (GBS e IGT). Los resultados (TABLA 1) obtenidos muestran que el mejor ajuste para los datos del IE lo brinda la distribución Weibull (HQIC= -2,157; AIC= -2,158; BIC= -2,155), seguida por la distribución Gamma (HQIC= -2,169, AIC= -2,170; BIC= -2,167).
|
|
Gamma |
Exponencial |
Lognormal |
Gaussiana Inversa |
Birbaum Saunders |
Weibull |
|
Log-verosimilitud |
4592,07 |
4686,99 |
4869,53 |
5691,14 |
5329,86 |
4566,57 |
|
p |
2 |
1 |
2 |
2 |
2 |
2 |
|
n |
2115 |
2115 |
2115 |
2115 |
2115 |
2115 |
|
HQIC |
-2,169 |
-2,215 |
-2,300 |
-2,689 |
-2,518 |
-2,157 |
|
AIC |
-2,170 |
-2,216 |
-2,301 |
-2,690 |
-2,519 |
-2,158 |
|
BIC |
-2,167 |
-2,214 |
-2,298 |
-2,687 |
-2,516 |
-2,155 |
P: cantidad de parámetros. n: cantidad de observaciones
TABLA 1: Criterios de Información para ajuste del IE con las distribuciones de vida más conocidas.
|
|
BSG |
|||
|
kernel Normal |
kernel Laplace |
kernel Logística |
kernel t-Student |
|
|
Log-verosimilitud |
5329,858 |
4857,106 |
4942,868 |
4760,090 |
|
p |
2 |
2 |
2 |
3 |
|
n |
2115 |
2115 |
2115 |
2115 |
|
HQIC |
-2,518 |
-2,295 |
-2,335 |
-2,248 |
|
AIC |
-2,519 |
-2,296 |
-2,336 |
-2,249 |
|
BIC |
-2,516 |
-2,293 |
-2,333 |
-2,246 |
TABLA 2: Criterio de Información para el ajuste del IE con las nuevas distribuciones BSG.
|
|
IGT |
|||
|
kernel Normal |
kernel Laplace |
kernel Logística |
kernel t-Student |
|
|
Log-verosimilitud |
5691,144 |
4826,096 |
4981,707 |
4640,726 |
|
p |
2 |
2 |
2 |
3 |
|
n |
2115 |
2115 |
2115 |
2115 |
|
HQIC |
-2,689 |
-2,280 |
-2,353 |
-2,191 |
|
AIC |
-2,690 |
-2,281 |
-2,354 |
-2,193 |
|
BIC |
-2,687 |
-2,278 |
-2,351 |
-2,189 |
TABLA 3: Criterio de Información para el ajuste del IE con las nuevas distribuciones IGT.
De la comparación de todos los ajustes, tanto de las figuras presentadas como de los valores obtenidos para los criterios de información, se consideraron únicamente las distribuciones Weibull y Gamma. Dado que estas dos distribuciones tienen la misma cantidad de parámetros y poseen parámetros de forma (Chen & Balakrishnan, 1995), para definir la elección entre ellas se utilizaron los estadísticos Cramér-von Mises y Anderson-Darling (distribuciones asimétricas con parámetros de forma). El estadístico de Anderson-Darling es de especial interés cuando importan las colas de una distribución, ya que les otorga más peso, como sucede en la evaluación de riesgos (Delignette-Muller & Dutang, 2015). El estadístico de Cramer-von Mises no considera la complejidad del modelo (es decir, el número de parámetros) lo cual no fue un problema ya que se compararon dos distribuciones que tienen la misma cantidad de parámetros como Weibull y Gamma (Delignette-Muller & Dutang, 2015).
Finalmente, se encontró que la distribución que mejor describe el comportamiento de los datos del IE es la distribución Weibull, ya que la misma presenta los menores valores de los estadísticos Cramer-von Mises y Anderson-Darling (TABLA 4).
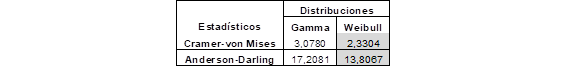
TABLA 4: Estadísticos Cramer-von Mises y Anderson-Darling para el ajuste del IE con las distribuciones Gamma y Weibull.
3.1.3 Validación de la distribución elegida con los gráficos TTT
Una propiedad interesante de la tasa de riesgo es que hace posible caracterizar el comportamiento de las distribuciones de vida. Diversos modelos de probabilidad que poseen densidades con formas similares, en algunos casos, tienen tasas de riesgo distintas, por lo que es muy importante tenerlas en cuenta para seleccionar o descartar distribuciones (Leiva et al., 2011). Estimar la tasa de riesgo es difícil. Una herramienta que permite determinar la forma de la tasa de riesgo es el gráfico TTT (del inglés, total time on test). Por medio de este gráfico se puede detectar el tipo de tasa de riesgo que tiene el índice IE (Aarset, 1987) y, de esta manera, se puede validar la distribución elegida.
En la TABLA 5 se resumen las formas de la tasa de riesgo correspondientes a los modelos más conocidos. Así, el gráfico TTT puede dar una indicación del tipo de distribución asociada con los datos (Leiva et al., 2011).
De esta manera, así como el gráfico Q-Qplot es útil para aproximar la distribución, el gráfico TTT puede indicar el tipo de distribución asociada con los datos (Vilca et al., 2010).
|
Forma del gráfico TTT |
Tasa de riesgo |
Modelos |
|
Curva cóncava |
Creciente |
Gamma y Weibull |
|
Curva convexa |
Decreciente |
Gamma y Weibull |
|
Curva cóncava, luego convexa |
Forma de bañera invertida |
Lognormal-BS IG-BSG |
|
Línea recta |
Constante |
Exponencial |
TABLA 5: Comportamiento de la tasa de riesgo según los modelos de distribución de variables de vida teóricos.
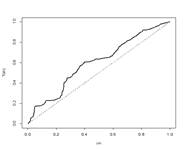
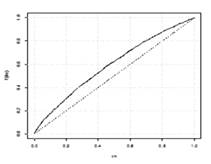
En la FIGURA 2, obtenida en el análisis de los datos, se observa que el comportamiento de la tasa de riesgo de los datos es creciente, lo cual valida la elección del modelo Weibull que se caracteriza por tener una tasa de riesgo creciente cuando su parámetro de escala es mayor a uno; en la estimación del IE el parámetro de escala es 3,66 lo que confirma la elección de este modelo.
|
TTT Plot de los datos del Índice de Intensidad IE |
TTT Plot de la distribución Weibull |
|
|
|
FIGURA 2: Comparación del TTT Plot de los datos del Índice de Intensidad con el TTT Plot de la Weibull.
Fuente: Elaborada a partir del paquete de lenguaje R “Adequacy Model”.
3.2 Construcción de una Escala Cualitativa
Para construir una escala cualitativa de niveles de riesgo se estimaron los percentiles poblacionales del índice IE a partir del modelo Weibull seleccionado.
Se definieron puntos de cortes en los percentiles estimados, 25% y 70% con los valores del índice 1,36 y 4,39 respectivamente, a los fines de conformar la escala del Índice de Nivel de Intensidad a la Exposición (TABLA 6). Con dichos puntos se definieron los grupos de exposición que clasifican a los agroaplicadores en baja, media y alta exposición (riesgo bajo, medio o alto, respectivamente), con el criterio establecido por el equipo de expertos de GEACC.
Finalmente, las categorías obtenidas son BAJO RIESGO hasta el valor del índice de 1,36; RIESGO MEDIO desde este valor hasta 4,39; y ALTO RIESGO a partir de 4,39.
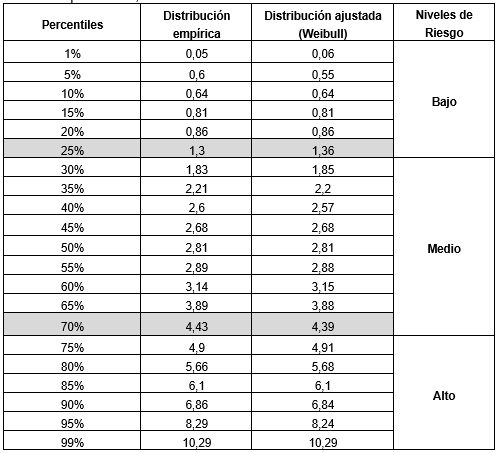
TABLA 6: Comparación de los percentiles de la distribución empírica del IE y los que resultan del ajuste con distribución Weibull.
3.2.1 Caracterización de los grupos de riesgo
A partir de la definición de los grupos de riesgo de exposición a los que pueden estar expuesto los agroaplicadores (Bajo, Medio y Alto), se analizaron diversas variables sociodemográficas, de estado y valoración de la salud; así como también se tomaron en cuenta las características o modalidad de la tarea que llevan a cabo como agroaplicadores con el fin de identificar diferencias entre los grupos de exposición. Se llevó a cabo un análisis descriptivo exhaustivo, obteniendo como principales resultados que el promedio de edad de los agroaplicadores es igual a 36 (D.E. 11,17) años con una dispersión relativa similar en todos los grupos (C.V. Bajo: 0,3066; C.V. Medio: 0,3052; C.V. Alto: 0,3091)[5]. En la TABLA 7 se observa que en el grupo de bajo riesgo se encuentran los agroaplicadores de menor edad (mínimo 14 años), mientras que los agroaplicadores de mayor edad se presentan en los grupos de riesgo medio y alto (máximo 88 y 87 años, respectivamente). En relación al nivel de educación, en todos los grupos, la mayor proporción de trabajadores cursó hasta el nivel secundario completo o incompleto y respecto al estado civil predominan los trabajadores casados o en concubinato.
|
Indicadores sociodemográficos |
Niveles de Riesgo de IE |
|||
|
Bajo |
Medio |
Alto |
||
|
Edad (años) |
Media DS Mínimo Máximo |
36,66 11,24 14 76 |
36,27 11,07 17 88 |
36,36 11,24 16 87 |
|
Nivel de Educacióna
|
Primario completo o Incompleto Secundario completo o incompleto Terc.-Univ. completo o incompleto |
40,08
42,41
17,51 |
40,04
47,72
12,24 |
42,29
44,67
13,04 |
|
Estado Civila
|
Soltero, separado o viudo
Casado o concubino
|
44,74
55,26 |
43,76
56,24 |
45,96
54,04 |
a Porcentaje de las categorías dentro de cada grupo.
TABLA 7: Estadísticos descriptivos de variables sociodemográficas.
Con respecto a la estadística descriptiva de las variables de salud (TABLA 8), en los tres grupos de riesgo predominan los trabajadores con dolor de cabeza o vértigo, los que nunca o raramente fueron hospitalizados y los que presentan con frecuencia o casi siempre signos de irritación. En el grupo de Riesgo Medio predominan los trabajadores que respondieron que nunca o raramente tienen cansancio excesivo o se sienten nerviosos o deprimidos. En los grupos de Bajo y Alto Riesgo hay mayor proporción de trabajadores que presentan mayor frecuencia (A veces, con frecuencia, casi siempre) de cansancio excesivo, o que se sienten nerviosos o deprimidos, siendo en ambos casos un poco mayor la proporción en el grupo alto.
|
Variable |
Categorías |
Niveles de Riesgo de IE |
||
|
Bajo |
Medio |
Alto |
||
|
Tiene dolores de cabeza o vértigosa |
Nunca o raramente
A veces, con frecuencia, casi siempre |
46,62
53,38
|
49,47
50,53
|
42,33
57,67 |
|
Está cansado excesivamentea |
Nunca o raramente
A veces, con frecuencia, casi siempre |
47,37
52,63 |
52,67
47,33 |
42,33
57,67 |
|
Se siente nervioso o deprimidoa |
Nunca o raramente
A veces, con frecuencia, casi siempre |
48,31
51,69 |
53,73
46,27 |
43,26
56,74 |
|
Fue hospitalizadoa |
Nunca o raramente
A veces, con frecuencia, casi siempre |
75,56
24,44 |
79,85
20,15 |
69,61
30,39
|
|
Tiene signos de irritacióna
|
Nunca o raramente
A veces, con frecuencia, casi siempre |
39,29
60,71
|
44,03
55,97 |
32,56
67,44 |
a Porcentaje de las categorías dentro de cada grupo.
TABLA 8: Estadística descriptiva de variables de salud.
En relación con la modalidad de la tarea realizada (TABLA 9), en todos los grupos de riesgo prevalecen: los que utilizan la receta proporcionada por el ingeniero agrónomo con la indicación de la dosis de plaguicida, los que no inyectan animales y los que mezclaron, aplicaron o estuvieron presentes cuando se manipulaban plaguicidas en un periodo menor o igual a 10 años.
|
Variable |
Categorías |
Niveles de Riesgo de IE |
||
|
Bajo |
Medio |
Alto |
||
|
Años que mezcló, aplicó o estuvo presentea |
Menor o igual a 10 Más de 10 años |
72,18 27,82 |
72,81 27,19 |
66,82 33,18 |
|
Inyecta animalesa
|
Sí No |
9,21 90,79 |
15,61 84,39 |
18,59 81,41 |
|
Utiliza receta de ingeniero agrónomoa |
Sí No |
83,96 16,04 |
87,88 12,13 |
82,16 17,84 |
a Porcentaje de las categorías dentro de cada grupo.
TABLA 9: Estadística descriptiva de variables de modalidad de la tarea.
Las variables detalladas en las TABLAS 7 a 9 se consideraron en la estimación de un modelo de regresión logística multinomial donde se tomó como referencia el grupo de riesgo Alto. En primer lugar, se eliminaron las variables con nivel de significación superior al 25% (edad, dolor de cabeza, hospital, nervioso o depresión y cansancio). Luego, se analizaron modelos alternativos comparando el cambio en la verosimilitud, a partir de los criterios BIC y AIC. El modelo finalmente seleccionado incluye las variables: Años que mezcló, aplicó o estuvo presente cuando se manipulaban plaguicidas, Inyecta animales, Utiliza receta de ingeniero agrónomo y presenta signos de irritación. En la TABLA 10 se presentan los resultados del modelo.
|
Niveles de Riesgo |
Variable |
Exp(β) |
Desvío Estándar |
p-valor |
Intervalo de Confianza 95% para Exp(β) |
|
|
Límite inferior |
Límite Superior |
|||||
|
Bajo Riesgo |
Años Mezcla |
1,24 |
0,1857 |
0,159 |
0,9202 |
1,6590 |
|
Inyecta |
2,27 |
0,4923 |
0,000 |
1,4794 |
3,4684 |
|
|
Receta Ingeniero |
0,90 |
0,1672 |
0,562 |
0,6230 |
1,2933 |
|
|
Irritación |
1,25 |
0,1744 |
0,113 |
0,9488 |
1,6414 |
|
|
Constante |
0,35 |
0,0807 |
0,000 |
0,2193 |
0,5471 |
|
|
Riesgo Medio |
Años Mezcla |
1,25 |
0,1634 |
0,085 |
0,9694 |
1,6172 |
|
Inyecta |
1,37 |
0,2273 |
0,055 |
0,9932 |
1,9002 |
|
|
Receta Ingeniero |
0,70 |
0,1178 |
0,033 |
0,5012 |
0,9717 |
|
|
Irritación |
1,45 |
0,1774 |
0,002 |
1,1449 |
1,8472 |
|
|
Constante |
0,94 |
0,1678 |
0,720 |
0,6586 |
1,3341 |
|
TABLA 10: Coeficientes del modelo multinomial de los grupos de riesgo, desvío estándar, nivel de significación (p-valor) e Intervalo de Confianza.
De los resultados presentados en la TABLA 10 se concluye que:
- Para la variable “Años que mezcló, aplicó o estuvo presente mientras se manipuló plaguicidas” aquellos que aplican o manipulan plaguicidas hace menos de 10 años tienen una chance 1,25 veces mayor (p-value: 0,085) de estar en el grupo de riesgo medio antes que, en el grupo de alto riesgo, que los que aplicaron hace más de 10 años.
- Los aplicadores que no inyectan animales tienen una chance 2,26 veces mayor de pertenecer (p-value: 0,000) al grupo de bajo riesgo antes que al de riesgo alto que los que inyectan animales. Esta chance disminuye a 1,37 veces en el grupo de riesgo medio respecto al de riego alto (p-value: 0,055).
- Los aplicadores que aplican sin receta de ingeniero agrónomo tienen una chance un 30,21% menor (p-value: 0,033) de estar en el grupo de riesgo medio antes que en el de alto riesgo, que los que tienen receta.
- Los aplicadores que nunca o raramente tengan signos de irritación tienen una chance 1,45 veces mayor (p-value: 0,002) de estar en el grupo de riesgo medio antes que en el de riesgo alto, que los que presentan signos irritativos frecuentemente.
En resumen, los factores que resultan significativos para determinar el riesgo de los aplicadores fueron: no tener receta de ingeniero agrónomo, inyectar animales, tener una antigüedad mayor a 10 años en las tareas de mezclar, aplicar o estar presente mientras se manipulan plaguicidas y la presencia de signos de irritación (TABLA 11).
|
Modalidad de la tarea |
Índice de Intensidad a la Exposición |
||
|
BAJO |
MEDIO |
ALTO |
|
|
Menos de 10 años que mezcló, aplicó o estuvo presente |
1,2355 [0,9202; 1,6590] |
1,2521** [0,9694; 1,6172] |
1 |
|
No Inyecta animales
|
2,2652* [1,4794; 3,4684] |
1,3738** [0,9932; 1,9002] |
1
|
|
No Utiliza receta de ingeniero agrónomo |
0,8976 [0,6230; 1,2933] |
0,6979* [0,5012; 0,9717] |
1 |
|
Nunca o raramente tiene signos de irritación |
1,2480 [0,9488; 1,6414] |
1,4543* [1,1449; 1,8472] |
1 |
* Diferencias significativas al 5%. ** Diferencias significativas al 10 %.
TABLA 11: Resumen de variables significativas del Modelo Multinomial ajustado para los grupos de riesgo
4. CONCLUSIONES
Dadas las características mencionadas en algunos casos se transforman los datos ambientales para eliminar la asimetría utilizando las transformaciones de Box-Cox y luego se ajusta a un modelo normal. A pesar del uso común de algunas transformaciones, se ha demostrado que una transformación incorrecta reduce la potencia del estudio. A veces, aunque una transformación se realice adecuadamente, el problema de la interpretación no se resuelve. Una forma alternativa de evitar la transformación de los datos ambientales es a través del ajuste a una distribución adecuada (Vilca et al., 2010).
Lo anterior otorga importancia a los nuevos modelos, IGT y BSG, que, a diferencia de las distribuciones tradicionales, permiten un mejor ajuste en las colas de la distribución; esto es importante cuando interesan los percentiles superiores, como en el caso del índice IE.
En este trabajo se propuso una secuencia de análisis para encontrar el mejor ajuste. A partir de un análisis gráfico de la distribución, se ajustaron los datos con las distribuciones recomendadas para este tipo de variables y, con el objeto de seleccionar uno de estos ajustes, se utilizaron los criterios de información y una validación final con los gráficos TTT. Esta secuencia propuesta puede ser de utilidad para estudios de índices similares.
El mejor ajuste para el IE se logró con la distribución Weibull, aunque cabe destacar que los nuevos modelos GBS e IGT con kernel t-Student se ajustaron mejor que cuatro de las distribuciones tradicionales Exponencial, Lognormal, Gaussiana Inversa y Birnbaum-Saunders. La distribución Weibull elegida fue validada analizando el comportamiento de la tasa de riesgo a partir de los gráficos TTT.
Una vez definido el mejor ajuste, se estimaron los percentiles utilizando un remuestreo Bootstrap, y a partir de los percentiles estimados se delimitaron tres niveles de riesgo (bajo, medio y alto). En función a estos niveles de riesgo se estudiaron características sociodemográficas y de salud de los trabajadores dentro de cada grupo. Los factores que resultaron más significativos para determinar el riesgo de los aplicadores fueron: la antigüedad (mayor a 10 años) en las tareas de mezclar, aplicar o estar presente mientras se manipulan plaguicidas, no tener receta del ingeniero agrónomo, inyectar animales y la presencia de signos de irritación.
Este indicador y su análisis, realizado por primera vez en Argentina, da lugar al inicio de un estudio predictivo ya que, dada las características de un nuevo trabajador, se puede determinar a qué grupo de riesgo pertenece y tomar las medidas preventivas necesarias logrando que se tome conciencia del peligro al que están expuestos y de esta manera se provean políticas públicas de prevención.
|
de variables de vida |
Función de Densidad Función de Distribución |
Tasa de riesgo |
|
Exponencial |
|
|
|
Weibull |
|
|
|
Gamma |
|
|
|
Lognormal |
|
|
|
Gaussiana Inversa |
|
|
|
Birnbaum-Saunders |
|
|
TABLA 12: Resumen de las distribuciones de probabilidad utilizadas en el ajuste distribucional del Índice del Nivel de Intensidad a la Exposición
5. REFERENCIAS
Aarset, M. V. (1987). How to identify a bathtub shaped hazard rate? IEEE Trans R 36,106-108.
Barros, M., Leiva, V., y Paula, G. (6 de mayo de 2008). Paquete de lenguaje R "gbs".
Bonner, M.R. y M.C.R. Alavanja (2005). The Agricultural Health Study Biomarker Workshop on Cancer Etiology. Introduction: Overview of Study Design, Results, and Goals of the Workshop. J Biochem Mol Toxicol 19(3): 169-171.
Chen, G., y Balakrishnan, N. (1995). A general purpose aproximate goodness-of-Fit Test. Journal of quality technology, 154.
Delignette-Muller, M. L., y Dutang, C. (2015). fitdistrplus: An R package for fitting distributions. Journal of Statistical Software, Volume 64, Issue 4.
Dirección de Estimaciones Agrícolas - Dirección Nacional de Agricultura. (2018). Estimaciones agrícolas. Obtenido de Ministerio de Agricultura, Ganadería y Pesca, Presidencia de la Nación: http://datosestimaciones.magyp.gob.ar/
Dosemeci, M., Alavaja, M.C.R., Rowland, A.S., Mage, D., Zahm, S. H., Rothman, N., Lubin, J.H., Hoppin, j. A., Sandler, D.P., Blair, A. (2002). A quantitative approach for estimating exposure to pesticides in the agricultural health study. The Annals of Occupational Hygiene, 46 (2): 245-260.
Lantieri, M., Butinof, M., R.A., F., Stimolo, M., Blanco, M., y Diaz, M. D. (2011). Work Practices, Exposure Assessment and Geographical Analysis of Pesticide Applicators in Argentina. Córdoba: Margarita Stoytcheva.
Leiva, V., Barros, M., Paula, G., y Saunders, S. (11 al 15 de agosto de 2010). Modelos de Daño Acumulativo Birbaum-Saunders y su Implementación en Código R. Simposio de Estadística 20 años. Santa Marta, Colombia.
Leiva, V., Hernández, H., y Sanhuenza, A. (20 de abril de 2008). Paquete de lenguaje R "ig".
Leiva, V., Soto, G., Cabrera, E., y Cabrera, G. (2011). Nuevas cartas de control basadas en la distribución. Revista Colombiana de Estadística, 34 (1), 147 a 176.
Marshal, A., y Olkin, I. (2007). Life Distributions. New York: Springer.
Vilca, F., Sanhuenza, A., Leiva, V., y Christakos, G. (2010). An extended Birnbaum-Saunders model and its application in the study of environmental quality in Santiago, Chile. Stoch Environ Res Risk Assess 24, 771-782.