Documento sin título

10.31047/1668.298x.v40.n2.40871

COMUNICACIÓN

Comparación de procedimientos de selección de variables para la modelación de la relación clima-patógenos en cultivos

F Suarez

C. Bruno

M. P Giménez Pecci

M. Balzarini

1 Suarez, F, (ORCID: 0000-0001-6763-7792): Instituto Nacional de Tecnología Agropecuaria (INTA), Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Unidad de Fitopatología y Mode-lización Agrícola (UFYMA), Córdoba, Argentina. Bruno, C., (ORCID: 0000-0002-3674-7128): Universidad Nacional de Córdoba, Facultad de Ciencias Agropecuarias, Instituto Nacional de Tecnología Agropecuaria (INTA), Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Unidad de Fitopatología y Modelización Agrícola (UFYMA), Córdoba, Argentina. Giménez Pecci, M. P. (ORCID: (ORCID: 0009-0007-6173-2845): Instituto de Patología Vegetal, Centro de Investigaciones Agropecuarias, Instituto Nacional de Tecnología Agropecuaria (INTA), Unidad de Fitopatología y Modelización Agrícola (UFYMA) , Córdoba, Argentina. Balzarini, M. (ORCID: 0000-00024858-4637): Universidad Nacional de Córdoba, Facultad de Ciencias Agropecuarias, Instituto Nacional de Tecnología Agropecuaria (INTA), Consejo Nacional de Investigaciones Científicas y Técnicas (CONI-CET), Unidad de Fitopatología y Modelización Agrícola (UFYMA), Córdoba, Argentina. Correspondencia a: suarezfranco@agro.unc.edu.ar

RESUMEN

Hoy es posible acceder fácilmente a cuantiosos volúmenes de datos climáticos georreferenciados. Éstos pueden ser usados para modelar la relación entre condiciones climáticas y enfermedad, para lo cual es necesario usar múltiples variables meteorológicas, usualmente correlacionadas y redundantes. La selección de variables permite identificar un subconjunto de regresoras relevantes para construir modelos predictivos. Stepwise, Boruta y LASSO son procedimientos de selección de variables de distinta naturaleza por lo que su desempeño relativo ha sido poco explorado. El objetivo de este trabajo fue la comparación de estos métodos aplicados simultáneamente en la construcción de modelos de regresión para predecir riesgo de enfermedad desde datos climáticos. Se utilizaron tres bases de datos georreferenciados con valores de presencia/ausencia de distintos patógenos en cultivos de maíz en Argentina. Para cada escenario se obtuvieron variables climáticas del periodo previo a la siembra hasta la cosecha. Con los tres métodos se generaron modelos predictivos con precisión de clasificación cercana al 70 %. LASSO produjo mejor predicción, seleccionando una cantidad intermedia de variables respecto a Stepwise (menor cantidad) y a Boruta (mayor). Los resultados podrían extenderse a otros patosistemas y contribuir a la construcción de sistemas de alarma basados en variables climáticas.

Palabras clave: LASSO, Stepwise, Boruta, regresión logística.

SUMMARY

Nowadays it is possible to easily access large volumes of georeferenced climatic data. These data can be used to model the relationship between climatic conditions and disease from múltiple meteorológica! variables, usually correlated and redundant. The selection of variables allows the identificaron of a subset of relevant regressors to build predictive models. Stepwise, Boruta, and LASSO are variable selection procedures of different nature, so their relative performance has been scarcely explored. The objective of this work was the comparison of these methods simultaneously applied in the construction of regression models to predict disease risk from climatic data. Three georeferenced databases were used with presence/absence values of different pathogens in maize crops in Argentina. For each scenario, climatic variables from the period prior to sowing until harvest were obtained. The three variable selection methods obtained models with accuracy close to 70 %. However, LASSO produced the best predictive model, selecting an intermediate number of variables with respect to Stepwise (lower number) and Boruta (higher number). The results could be extended to other pathosystems and inspire the construction of alarm systems based on climatic variables.

Keywords: LASSO, Stepwise, Boruta, logistic regression.

INTRODUCCION

El desarrollo epidemiológico de las enfermedades infecciosas resulta de la interacción de al menos tres factores principales: un ambiente conductivo (condiciones meteorológicas), un huésped susceptible y un patógeno virulento (Ortiz et al., 2022). El conocimiento sobre las condiciones meteorológicas que predisponen a la presencia de enfermedades puede ser utilizado para mejorar la toma de decisiones en la producción, reducir pérdidas y predecir posibles brotes de la enfermedad en diferentes condiciones ambientales. En la actualidad es posible acceder de manera simple y económica a cuantiosos volúmenes de datos climáticos georreferenciados, provenientes de imágenes o productos satelitales desde distintas plataformas (Paccioretti et al., 2023). Con la creciente disponibilidad de datos climáticos se han generado nuevos modelos basados en la relación entre las condiciones ambientales y la enfermedad o los vectores de enfermedades, que luego pueden ser usados para predecir incidencia en el patosistema. Se pueden citar ejemplos como el de la predicción de la incidencia de la roya del café, del tizón tardío en papa, de la severidad de GDMV (grape downy mildew en vid) y de distintas especies de begomo-virus en cultivos de soja (Glycine max L.) y poroto (Phaseolus vulgaris L.) (Chenid et al., 2020; Lasso et al., 2020; Ortiz et al., 2022; Reyna et al., 2023). El maíz (Zea mays L.) es uno de los cultivos más importantes porque se utiliza en la dieta humana, animal y para la producción de biocombustibles (López-Ramírez et al., 2022). En el ciclo agrícola 2021/2022 la producción de maíz en Argentina fue de 52 millones de toneladas (Bolsa de Cereales, 2021). La producción de maíz se ve afectada por varios patógenos que causan diferentes enfermedades (Rossi et al., 2019). Los agentes patógenos más frecuentes son hongos y virus (Ruiz et al., 2021), aunque también se encuentran infecciones bacterianas (López-Ramírez et al., 2022) y por spi-roplasmas (Barontini et al., 2022). La resistencia genética es un método rentable y ambientalmente racional para minimizar las pérdidas causadas por las enfermedades del maíz. Sin embargo, obtener genotipos con resistencia efectiva, duradera y de amplio espectro, siempre es un desafío (Rossi et al., 2019) dado que se basan en la relación genotipo-enfermedad, y lo poco que se ha explorado de la relación clima-enfermedad para nuestra región, a excepción de algunos trabajos relacionados al uso de información climática para predecir riesgo de infección por el Mal de Rio Cuarto (March et al., 1995). Independientemente del cultivo y patógeno que se quiere estudiar, cuando se requiere modelar la relación de una enfermedad con el clima aparece el desafío de trabajar con múltiples parámetros climáticos, usualmente correlacionados y redundantes.

El rendimiento de los modelos predictivos, en términos de sesgos y eficiencia estadística, depende de las variables que ingresan en las ecuaciones que se estiman, de la precisión de las estimaciones de los parámetros asociados a cada una de esas variables (Chenid et al., 2020) y de los tamaños muestrales usados. Dada la gran cantidad de variables climáticas disponibles para determinar cuál condición climática y en qué período del cultivo es útil como entrada al modelo que se desarrollará para la predicción de la presencia de una respuesta epidemiológica, necesariamente se requiere la implementación (previa o simultánea) de un proceso de selección de variables. La selección de variables es el proceso que determina el subconjunto de variables relevantes para construir modelos robustos. El proceso de selección de variables, en general, tiene cuatro etapas: generación de subconjuntos de variables predicto-ras, evaluación de los subconjuntos, criterios de parada o detención del proceso y validación de resultados logrados con los conjuntos de predic-toras seleccionados (Rostami et al., 2021). La reducción de la dimensionalidad lograda al eliminar características irrelevantes y redundantes permite reducir la complejidad computacional y mejorar el rendimiento del modelo (Rostami et al., 2021). La comparación de los procedimientos o algoritmos disponibles para la selección de variables provee información relevante para los modelistas, ya sea que trabajen en el campo disciplinar estadístico clásico o con predictores derivados por técnicas de aprendizaje automático, común en ciencia de datos en contextos con numerosos parámetros y alta disponibilidad de datos.

Además de los modelos de regresión múltiple estimados desde procedimientos estadísticos, los modelos predictivos obtenidos con métodos de aprendizaje automático (AA) han demostrado buenos rendimientos para la predicción, por lo que existen numerosos procedimientos de AA para la selección de variables (Li et al., 2019; Witten et al., 2016). Los métodos de AA proporcionan un marco poderoso y flexible no solo para la toma de decisiones basada en datos, sino también para la incorporación de conocimiento experto en el sistema.

La regresión paso a paso (Stepwise), es una técnica ampliamente utilizada para la selección de variables y el modelado estadístico. Aun cuando el método ha sido criticado por producir valores de significancia estadística sesgados (Whittingham et al., 2006), algunos resultados recientes donde se trabaja con algoritmos envolventes (i. e. selección, prueba de modelo, selección y así sucesivamente) han mostrado que tiene propiedades deseables (Zogata-Siudem y Jaroszewicz, 2021). La regresión Stepwise hacia adelante (Forward) acoplada al uso de criterios estadísticos como el factor de inflación de la varianza (VIF) para detectar multicolinea-lidad, y el uso del p valor para detectar falta de significancia estadística (Stepwise+VIF+p-Valor) resultó el mejor procedimiento cuando se lo comparó con otros algoritmos de AA que utilizan un proceso iterativo para ir descartando las predicto-ras menos relevantes (Suarez et al., 2023). Sin embargo, la selección de variables predictoras para un modelo de regresión en contexto de conjuntos de variables de alta cardinalidad también puede ser abordada desde métodos estadísticos “de re-gularización" como Ridge (Hoerl y Kennard, 1970; Tikhonov, 1963) o LASSO (por sus siglas en inglés, Least Absolute Shrinkage and Selection Operator) (Fonti y Belitser, 2017; Shafiee et al., 2021; Tibshi-rani, 1996). Los métodos de regularización usan todas las variables, pero con distintos pesos tendiendo a que los coeficientes del modelo se aproximen a cero a una velocidad mayor cuando las variables tienen poca capacidad predictiva. Así, el método Ridge y el método Lasso minimizan el riesgo de sobreajuste, reducen la varianza, atenúan el efecto de la correlación entre predictoras y reducen la influencia en el modelo de las predictoras menos relevantes. Particularmente LASSO, basado en un modelo de regresión lineal múltiple, penaliza el valor absoluto de los coeficientes de regresión (restricción l₁), de manera que cuanto mayor es la penalización, mayor será la reducción de los coeficientes, y algunos llegarán a 0, eliminando automáticamente las covariables innecesarias/no influyentes (McEligot et al., 2020; Rusyana et al., 2021). Para el AA la selección de características con capacidad predictiva constituye el mayor desafío en problemas de alta dimensio-nalidad. Existen diversos métodos de selección de variables (Jovi et al., 2015; Peres y Fogliatto, 2018), entre los que provienen del AA se pueden citar el método Boruta (Kursa y Rudnicki, 2010) y el algoritmo genético (García-Dominguez et al., 2020). El objetivo de este trabajo fue comparar el desempeño de procedimientos de selección de variables de distinta naturaleza en contexto de modelación para predecir riesgos de enfermedad en cultivo desde un conjunto de variables climáticas de alta dimensionalidad.

MATERIAL Y MÉTODOS

Datos

Las bases de datos utilizadas en este trabajo fueron tres y se han conformado con registros provenientes del monitoreo de enfermedades en cultivos de maíz (Zea mays L.) a lo largo de la región maicera argentina. En cada lote se muestrearon plantas con síntomas de enfermedad (o infección) que fueron llevadas al laboratorio para determinar si el patógeno estaba presente, generando bases de datos de presencia o ausencia de cada patógeno a la que se adicionaron múltiples registros de variables climáticas de presiembra e inicio del cultivo. Para estas muestras no se contó con información referida a la aplicación de algún tipo de control de vectores. Debido a la falta de información sobre las variedades de cultivo en el 80 % de las muestras, no se incluyó esta variable en el análisis.

Base de datos 1: Aspergillus flavus

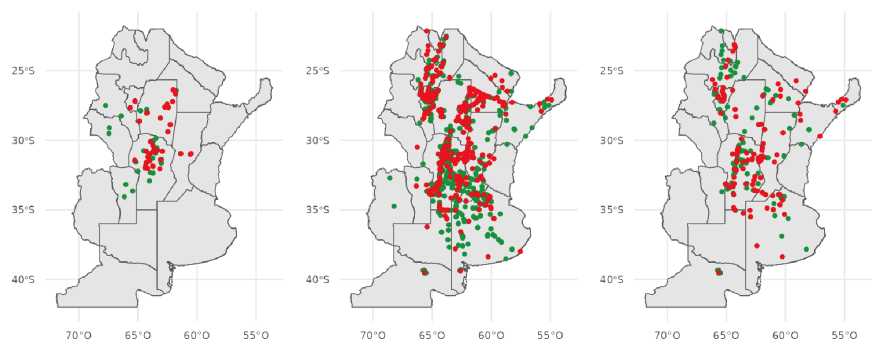
Contiene un total de 223 observaciones georre-ferenciadas con datos de presencia o ausencia del hongo Aspergillus flavus. Los puntos mues-treados corresponden a la región delimitada entre la longitud 67,73° y 60,50° O y la latitud 34,06° y 26,38° S (Figura 1, izquierda). Los muestreos de los lotes se llevaron a cabo entre los ciclos agrícolas 2012/2013 a 2019/2020. Además, se incluyeron los valores de humedad relativa, temperatura, precipitaciones acumuladas, velocidad del viento resumidas semanalmente para el período de 39 semanas, que comienza ocho semanas antes de la fecha de siembra y finaliza tres semanas después de fecha de cosecha, sumando 156 variables bio-climáticas. La dimensión de la base fue de 223 filas x 156 columnas. También, se contó con la variable categórica fecha de siembra (siembra temprana o siembra tardía).

Base de datos 2. Corn stunt spiroplasma (CSS)

Contiene un total de 1939 observaciones de presencia o ausencia de CSS. Los puntos mues-treados corresponden a la región comprendida entre la longitud 68,58° y 54,90° O y la latitud 39,55° y 22,14° S (Figura 1, centro). Los muestreos de los lotes se llevaron a cabo entre los ciclos agrícolas 1997/1998 a 2021/2022. En cuanto a las variables climáticas se incluyeron los valores mensuales de humedad relativa, precipitaciones, punto de rocío, temperatura, total de evaporación y velocidad del viento para los meses de agosto a abril, totalizando 54 variables bioclimáticas. La dimensión de la base fue de 1939 filas x 54 columnas.

Figura 1: Puntos de muestreo de cada base de datos. Aspergillus flavus (Izquierda); CSS (centro); MDMV (derecha). Puntos verdes indican ausencia del patogeno. Puntos rojos indican presencia del patogeno.

Base de datos 3: Maize dwarf mosaic virus (MDMV)

La base cuenta con 291 observaciones de presencia o ausencia de MDMV Los puntos muestrea-dos corresponden a la región comprendida entre la longitud 66,18° y 54,90° O y la latitud 39,55° y 22,14° S (Figura 1, derecha). Los muestreos de los lotes se llevaron a cabo entre los ciclos agrícolas 1999/2000 a 2021/2022. Se incluyeron los valores mensuales de humedad relativa, precipitaciones, punto de rocío, temperatura, total de evaporación y velocidad del viento para los meses de agosto a abril, totalizando 54 variables bioclimáticas. La dimensión de la base fue de 291 filas x 54 columnas.

Procedimientos de selección de variables y ajuste de modelo predictor

Stepwise Forward

El proceso se inicia generando el modelo sin predictoras (M₀). Luego, se generan todos los posibles modelos que se pueden crear añadiendo de a un predictor al M₀. De entre todos estos modelos con una predictora se selecciona el mejor basándose en el error de entrenamiento, al modelo elegido se denomina M₁. Se repite el paso anterior, pero esta vez partiendo del último modelo seleccionado y así sucesivamente hasta llegar al modelo con todos las predictoras. De los mejores modelos seleccionados para cada número de predictoras (M₀,M₁,M₂,^, M_k) se identifica el mejor, empleando una métrica de validación (Horton y Kleinman, 2015; Rodrigo, 2016). Aún pueden quedar predictoras redundantes y para eliminarlas se pueden usar criterios estadísticos como VIF (variance in-flation factor) y p-valor (Balzarini et al., 2008). Para reducir problemas de multicolinealidad entre las variables, aplicamos el criterio VIF asociado a los coeficientes de la regresión con mejor subconjunto de variables obtenido y se eliminaron las variables con un VIF mayor a 5, valores mayores de VIF sugieren correlación entre predictoras (Vu et al., 2015). Por último, se eliminaron las variables que no resultaron significativas en el modelo (p-valor > 0,05).

La selección Stepwise Forward se implementó mediante la función train, disponible en el paquete caret del sofware R (R Core Team, 2022), con los siguientes argumentos: method = “glmStepAIC”, family = “binomial”, direction = “forward”, metric = “Accuracy”, steps = 1000. Al definir method = “glmStepAIC” el método ajusta el modelo predicti-vo con una regresión logística.

Boruta

Es un algoritmo de aprendizaje automático (AA) de tipo envolvente usualmente basado en el algoritmo de predicción de AA conocido como Random Forest (Kursa y Rudnicki, 2010), aunque es posible trabajar con cualquier método de clasificación que pueda aplicar medidas de importancia de las entradas o predictoras. En los métodos de tipo envolvente se utiliza un subconjunto de funciones para entrenar un modelo y con base en la inferencia del modelo ajustado se decide agregar o eliminar variables del subconjunto (Li et al., 2014; Maldonado et al., 2015). En el algoritmo Boruta las variables no compiten entre sí, sino con una versión aleatoria de ellas, estas variables se denominan variables sombra. Boruta ajusta un algoritmo de predicción o clasificación de AA capaz de capturar relaciones e interacciones no lineales y luego extrae la importancia de cada variable en el predictor conservando sólo aquellas que están por encima de un umbral de importancia determinado. El umbral se define como la mayor importancia de variable registrada entre las variables sombra. Es decir que una variable es útil solo si es capaz de funcionar mejor que la mejor selección aleatoria. En cada iteración, Boruta verifica si la variable medida tiene mayor importancia que la mejor de sus variables sombra y elimina las variables que se consideran poco importantes. Finalmente, el algoritmo se detiene cuando se confirman o rechazan todas las variables o cuando alcanza un límite especificado para la precisión de la predicción (Gholami et al., 2021) . La selección mediante Boruta se implementó desde la función boruta del paquete Boruta (Kursa y Rudnicki, 2010) del software R (R Core Team, 2022) , con los siguientes argumentos: maxRuns = 1000, doTrace = 3, pValue = 0,01, getImp = ge-tImpRfZ.

Finalmente, las variables que se confirmaron como importantes fueron incluidas en una regresión logística. La regresión fue ajustada con la función train del paquete caret (Max Kuhn, 2021) del software R, con los siguientes argumentos: method = “glm”, family = “binomial”, metric = “Accuracy”. Al definir method = “glm”, family = “binomial” el método ajusta una regresión logística.

LASSO

Es un método de regularización. Genera una restricción o penalización en algunos valores absolutos de los coeficientes del modelo forzando a que las estimaciones de los coeficientes tiendan a cero. LASSO penaliza la suma del valor absoluto de los coeficientes de regresión. A esta penaliza-ción se la conoce como l₁ y tiene el efecto de forzar a que los coeficientes de las predictoras tiendan a cero. Dado que un predictor con coeficiente igual a cero no influye en el modelo, LASSO consigue excluir las variables menos relevantes. Al igual que Ridge, el grado de penalización está controlado por el hiperparámetro X. Cuando X = 0, el resultado es equivalente al de un modelo de regresión lineal estimado por mínimos cuadrados. A medida que X aumenta, mayor es la penalización y más predictoras quedan excluidas. Así, el hiperparámetro X es un parámetro de ajuste (Hastie et al., 2020). LASSO es un método que realiza tanto la selección de características como el ajuste del modelo de regresión o clasificación.

En este trabajo LASSO se implemento mediante la función train del paquete caret(Max Kuhn, 2021) del software R, con los siguientes argumentos: method = “glmnet”, metric = “Accuracy”, family = “binomial”. Al definir method = “glmnet”, family = “binomial” el método ajusta una regresión logística. El parámetro se determinó mediante una búsqueda en grilla con la función expand.grid, en donde se probaron 1001 valores desde 0 a 1 cada 0,001.

Criterios de comparación del desempeño estadístico. Validación

Cada base de datos fue particionada en dos subconjuntos de datos, uno para entrenamiento (80 % de los datos) y otro para validación (20 % de los datos). Para seleccionar las variables y ajustar los modelos se utilizó la base de entrenamiento con una validación cruzada repetida de k = 10 y con 5 repeticiones, la cual utiliza el valor de la precisión para elegir el mejor modelo, y en el caso de LASSO también elige valor óptimo de X. Posteriormente cada regresión logística fue validada con la base de validación y se compararon, entre los métodos, los valores de precisión, sensibilidad, especificidad y área bajo la curva (AUC) de una curva ROC (Receiver Operating Characteristics) la cual relaciona la sensibilidad o la tasa de verdaderos positivos del clasificador con la especificidad o la tasa de verdaderos negativos. Entre los índices resumen de la curva ROC, el AUC es utilizado para la comparación de modelos (Yin et al., 2021). Bajo la hipótesis nula, el modelo clasificador no supera a la clasificación azarosa y el área sería 0,5. Cuanto mayor sea el área, mejor será la capacidad de discriminación. Se suelen utilizar valores de AUC de 0,70-0,79, 0,80-0,89 y >0,90 para representar una capacidad discriminatoria regular, excelente y sobresaliente, respectivamente (Hosmer y Le-meshow, 2000). Las cantidades necesarias para construir la curva ROC se obtuvieron de una matriz de confusión donde se comparan los valores observados (grupo de pertenencia) con los valores predichos (grupo al que se asigna la observación). La matriz de confusión se calculó mediante la función confusionMatrix del paquete caret (Max Kuhn, 2021) del software R. El script se encuentra disponible en https://github.com/FrancoMSuarez/ FeatureSelection

RESULTADOS Y DISCUSIÓN

La motivación detrás de los procedimientos de selección de variables es la selección cuasiauto-mática de subconjuntos de variables no redundantes que sean más relevantes para el problema de predicción/clasificación. Eliminando variables irrelevantes se mejora la eficiencia computacional y se reduce el error de generalización del modelo (Heinze et al., 2018). Un método de selección de variables se puede evaluar desde dos aspectos: la eficiencia y la eficacia. La eficiencia de un método de selección de características depende del tiempo requerido para encontrar el subconjunto de características finalmente seleccionado. Mientras que la efectividad depende de la calidad del subconjunto de variables seleccionado (Rostami et al., 2021). En este trabajo nos centramos particularmente en la efectividad de los diferentes métodos de selección de variables, por lo cual se evaluaron los métodos en términos del número de variables seleccionadas y la precisión de clasificación. Si bien, la cantidad de variables seleccionadas depende usualmente de características de la base de datos, los resultados muestran que el método Bo-ruta fue el que más porcentaje de variables seleccionó en las tres bases de datos que se utilizaron como ejemplo en este trabajo (Tabla 1).

En el caso de la base CSS, el algoritmo Boruta seleccionó el 100 % de las variables bioclimáticas de la base. En el trabajo llevado a cabo por Shi et al. (2019) Boruta también seleccionó todas las variables en más del 80 % de las permutaciones realizadas para evaluar la clasificación. Nilsson et al. (2007) plantean que una variable es relevante si la información que aporta no puede ser explicada u obtenida por ninguna otra y que las variables poco relevantes aportan información redundante. Encontrar todos los atributos que en algunas circunstancias son relevantes para la clasificación, en lugar de solo los no redundantes, hace que al aplicar Boruta a un conjunto de datos con alta cantidad de variables correlacionadas, la selección pueda ser del 100 %.

Tabla 1: Cantidad de variables climáticas seleccionadas por cada método en bases de datos de tres patosistemas

Sin embargo, el número de variables a seleccionar por LASSO, depende del valor que asuma el parámetro (Hastie et al., 2020), mientras más grande el valor de mayor será la selección. En la base de A. flavus el valor del optimizado fue de 0,11, para la base de CSS fue igual a 0,001 y para MDMV 0,064. Con estos valores se logró la mejor precisión en cada una de las bases de datos (Figura 2). En este trabajo la metodología Step+VIF+pValor fue el método que redujo más fuertemente la cantidad de variables predictoras.

En cuanto a la precisión de la clasificación, en el subconjunto de cada base que se utilizó para la selección de variables y entrenamiento de los modelos logísticos, observamos que LASSO obtuvo los mayores valores de precisión en dos de las tres bases de datos (Tabla 2) y fue similar a los otros métodos en la base MDMV que se caracteriza por tener un bajo número de observaciones. En las simulaciones llevadas a cabo por Singh (2021) se demostró que LASSO se desempeñó peor que Stepwise, cuando se aplica a bases con pocas muestras.

Cuando evaluamos el desempeño diagnóstico de los modelos en las tres muestras de validación externa pudimos observar que LASSO fue superior en las tres bases de datos (Tabla 3). También se evaluó la capacidad del modelo de clasificación usando el área bajo la curva ROC. En la base de MDMV, LASSO presentó un área bajo la curva mayor a Step+VIF+pValor y Boruta (Figura 3, derecha), mientras que, en la base de CSS, LASSO obtuvo un área bajo la curva muy similar a Boruta, y Step+VIF+pValor fue el de menor AUC (Figura 3, centro) y en la base de A. flavus LASSO obtuvo la mayor AUC y Step+VIF+pValor la menor.

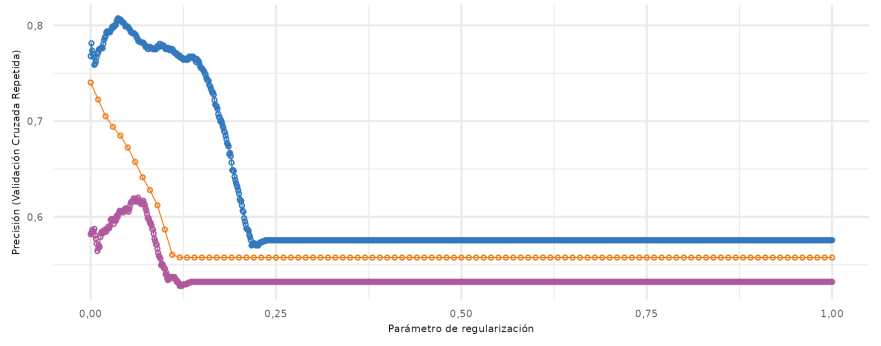
Figura 2: Optimización del parámetro de regularización ( ^) para tres bases de datos. Azul: A. flavus, naranja: CSS, magenta: MDMV.

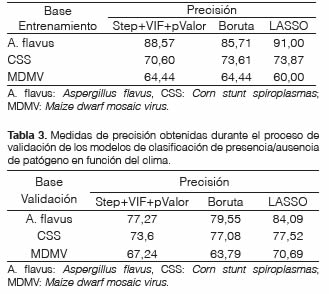
Tabla 2: Medidas de precisión obtenidas durante el proceso de selección y entrenamiento de los modelos de clasificación de presencia/ausencia de patógeno en función del clima

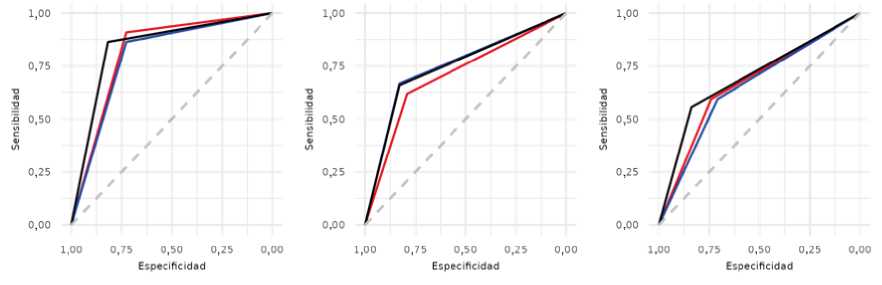
Figura 3: Curvas ROC. Derecha: MDMV, Centro: CSS, Izquierda: A. flavus. Curva roja: Step+VIF+pValor, curva negra: LASSO, curva azul: Boruta.

La selección Step+VIF+pValor pudo llegar a modelos óptimos consiguiendo un buen rendimiento computacional y evitando el sobreajuste. Step+VIF+pValor puede verse como una versión “optimizada localmente” del mejor subconjunto de predictoras, actualizando el conjunto activo de a una variable en cada paso, en lugar de optimizar sobre todos los subconjuntos posibles de un tamaño dado. LASSO se puede entender como una versión más “democrática” de Stepwise, ya que actualiza los coeficientes de regresión de cada variable de manera de obtener la misma correlación entre las variables y los residuos (Hastie et al., 2020).

En términos de evaluar los métodos en cuanto a su efectividad, LASSO seleccionó un número de variables mayor que Step+VIF+pValor, pero menor a Boruta y presentó la mayor precisión en las tres bases de datos empleadas. Cabe destacar algunas limitaciones de LASSO que se han observado en conjuntos de datos de n pequeño y p sustancialmente más grande. En tales escenarios, LAS-SO seleccionará como máximo n variables antes de saturarse y si hay variables agrupadas (altamente correlacionadas entre sí), LASSO tenderá a seleccionar una variable de cada grupo ignorando las demás (Fonti, 2017). El método denominado ElasticNet (Zou y Hastie, 2005) trata de una extensión que se logra al combinar LASSO con RIDGE que podría superar las limitaciones de LAS-SO (no incluido en el trabajo). LASSO seleccionó mayor número de variables en comparación con Step+VIF+pValor, hecho que reduce la probabilidad de eliminación de variables con potencialidad predictiva y potencia la precisión del modelo. Sin embargo, también se retienen variables no relacionadas significativamente con la variable respuesta, por lo que es difícil interpretar los resultados en función de la selección de potenciales predictoras. La comparación de los procedimientos de selección de variables es multicriterio, aunque principalmente discutida en términos de precisión del clasificador obtenido para predecir presencia/ausencia del agente patógeno en función del clima. Los modelos validados para A. flavus y CSS presentaron buenas métricas cuantitativas. Las variables climáticas seleccionadas para ajustar el modelo predic-tivo fueron distintas para cada base (Figura 4).

Para el caso de A. flavus, las variables que fueron seleccionadas por los métodos Step+VIF+pValor y LASSO fueron humedad relativa en la semana 15 y temperatura en la semana 19. Para CSS el método Step+VIF+pValor seleccionó varias variables: velocidad viento de abril, humedad relativa y total de evaporación de agosto, temperatura de septiembre, velocidad de viento y precipitaciones de octubre, humedad relativa de diciembre, precipitaciones y punto de rocío de febrero, precipitaciones y velocidad viento de marzo. Todas esas variables (excepto humedad relativa de agosto) también fueron seleccionadas por el método LASSO. Para MDMV las variables seleccionas por ambos métodos coincidieron en la humedad relativa de agosto, evaporación de diciembre y las precipitaciones de marzo. Se presentan todas las variables seleccionadas por Step+VIF+pValor y LASSO en cada base de datos, y el valor estimado de los coeficientes de cada variable (Figura 4).

La presencia de enfermedades en un lote agrícola está influenciada por las condiciones climáticas, que favorecen el desarrollo de patógenos, y también por la resistencia/susceptibilidad genética de las plantas a la infección. Aunque las condiciones ambientales sean favorables, la infección puede no ocurrir si las plantas tienen resistencia genética al patógeno o si se han aplicado controles químicos. En este estudio, se utilizaron plantas recolectadas en lotes muestreados a través de distintos ciclos agrícolas para ilustrar y validar los métodos de selección de variables. La ausencia de registros sobre controles químicos y sobre la genética impidieron considerar estas variables en nuestro análisis. Esto no impide la comparación de los métodos de selección de variables, pero podría influir en la elección de las variables predictoras que se consideren útiles para predecir futuras infecciones si se confunden los efectos de la genética y el ambiente. Es importante mencionar que el riesgo de confusión es menor en estudios observacionales con bases de datos más grandes, ya que las observaciones se incrementan. Si existen datos sobre el manejo de los lotes, estos pueden ser incluidos como variables en el modelo o utilizados para filtrar los datos y seleccionar lotes con información más clara sobre la relación entre el clima y la enfermedad. En este trabajo, se ha evaluado el desempeño de los métodos de selección de variables considerando únicamente las variables climáticas, sin tener en cuenta otras variables potenciales como el manejo o la genética de los cultivos.

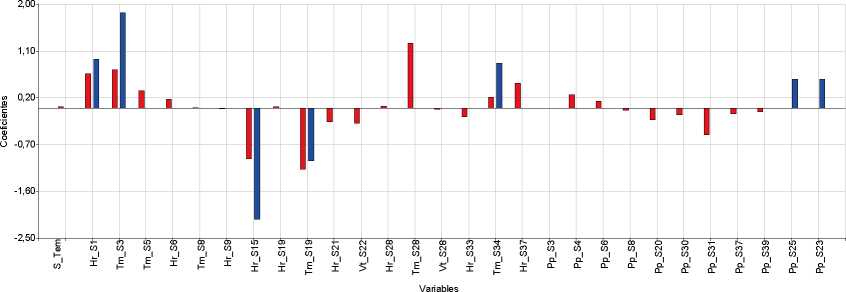
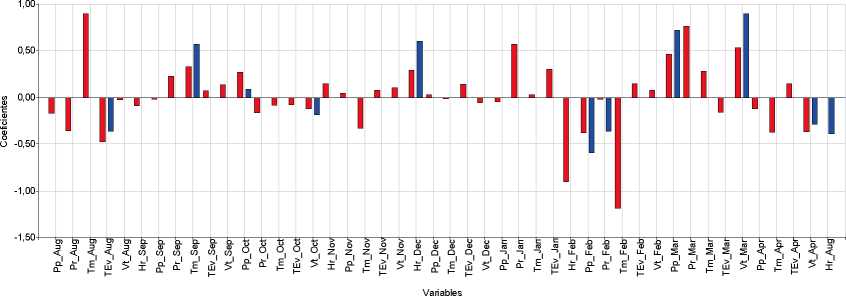
Figura 4: Variables seleccionadas y coeficiente de regresión estimado por los métodos Step+VIF+pValor y LASSO. Barras Azules: Variables seleccionadas por Step+VIF+pValor. Barras Rojas: Variables seleccionadas por LASSO. Arriba: Aspergillus flavus. Centro: Corn stunt spiropiasmas. Abajo: Maize dwarf mosaic virus. S_Tem: Siembra Temprana, Hr_Semana: Humedad relativa de la semana, Tm_Semana: Temperatura media de la semana X, Vt_Semana: Velocidad del viento de la semana X, Pp_Semana: Precipitaciones de la semana X. Pp_mes: precipitaciones del mes X, Tm_mes: temperatura del mes X, TEv_mes: total de evaporación del mes X, Vt_mes: velocidad del viento del mes X, Hr_mes: humedad relativa del mes X, Pr_mes: punto de rocío del mes X.

CONCLUSIÓN

El modelo construido a partir del método de selección de variables LASSO para clasificar sitios según riesgo de enfermedad del cultivo de maíz en función de variables climáticas, mostró tener mayor poder predictivo para discernir entre presencia y ausencia del agente patógeno en el cultivo. LAS-SO produjo una parametrización intermedia entre los métodos de selección Step+VIF+pValor (mínima cantidad de predictoras) y Boruta (máxima cantidad de predictoras). Estos resultados podrían extenderse a otros patosistemas.

AGRADECIMIENTOS

Las investigaciones que sustentan este estudio fueron posibles gracias al proyecto PUEDD UFY-MA-CONICET (2019-2023 N.° 22920180100064 CO). Se agradece especialmente a investigadoras de la Unidad de Fitopatología y Modelización Agrícola (UFYMA) quienes recolectaron los datos que sirvieron como ilustración/validación: a Ada Karina Torrico por brindar la base de Aspergillus flavus y a María de la Paz Giménez, por construir la base de CSS y MDMV.

Fecha de recepción: 04/04/2023

fecha de aceptación: 20/10/2023

BIBLIOGRAFÍA

Amat Rodrigo, J. (2016). Introducción a la Regresión Lineal Múltiple. Ciencia de Datos blog. https://www. cienciadedatos.net/documentos/25 regresion lineal multiple

Balzarini, M. G., González, L., Tablada, M., Casanoves, F., Di Rienzo, J. A. y Robledo, C. W. (2008). Infostat. Manual del Usuario, Editorial Brujas.

Barontini, J. M., Malavera, A. P., Ferrer, M., Torrico, A. K., Maurino, M. F., y Giménez Pecci, M. P (2022). Infection with Spiroplasma kunkelii on temperate and tropical x temperate maize in Argentina and development of a tool to evaluate germplasm. European Journal of Plant Pathology, 162(2), 455-463. https://doi.org/10.1007/ s10658-021-02415-4

Bolsa de Cereales de Buenos Aires (2021). Informe cierre de campaña. Maíz 2021-2022. https://www.bolsade-cereales.com/estimaciones-informes

Chen, M., Ois Brun, F., Raynal, M. y Makowski, D. (2020). Forecasting severe grape downy mildew attacks using machine learning. PLOS ONE 15(3), e0230254. https://doi.org/10.1371/iournal.pone.0230254

Fonti, V. (2017). Research paper in business analytics: feature selection with LASSO. VU Amsterdam research paper in business analutics, 30, 1-25.

García-Dominguez, A., Galván-Tejada, C. E., Zanella-Cal-zada, L. A., Gamboa-Rosales, H., Galván-Tejada, J. I., Celaya-Padilla, J. M., Luna-García, H. y Magallanes-Quintanar, R. (2020). Feature Selection Using Genetic Algorithms for the Generation of a Recognition and Classification of Children Activities Model Using Environmental Sound. Mobile Information Systems, Volume 2020, 8617430. https://doi.org/10.1155/2020/8617430

Gholami, H., Mohammadifar, A., Golzari, S., Kaskaoutis, D. G. y Collins, A. L. (2021). Using the Boruta algo-rithm and deep learning models for mapping land susceptibility to atmospheric dust emissions in Iran. Aeo-lian Research, 50, 100682. https://doi.org/10.1016/¡.aeolia.2021.100682

Hastie, T., Tibshirani, R. y Tibshirani, R. (2020). Best Subset, Forward Stepwise or Lasso? Analysis and Recommendations Based on Extensive Compari-sons. Statistical Science, 35(4), 579-592. https://doi. org/10.1214/19-STS733

Heinze, G., Wallisch, C. y Dunkler, D. (2018). Variable selection - A review and recommendations for the prac-ticing statistician. Biometrical Journal, 60(3),431-449. https://doi.org/10.1002/bim¡.201700067

Hoerl, A. E. y Kennard, R. W. (1970). Ridge regression: Biased Estimation for Nonorthogonal Problems. Tech-nometrics, 12(1), 55-67. https://doi.org/10.1080/00401 706.1970.10488634

Horton, N. J. y Kleinman, K. (2015). Using R and RStudio for Data Management, Statistical Analysis, and Graphics. CRC Press.

Hosmer, D. W. y Lemeshow, S. (2000). Applied Logistic Regression. John Wiley & Sons.

Jovi , A., Brki , K. y Bogunovi , N. (2015). A review of feature selection methods with applications. 2015 38th International Convention on Information and Com-munication Technology, Electronics and Microelec-tronics (MIPRO), 1200-1205. https://doi.org/10.1109/ MIPRO.2015.7160458

Kursa, M. B. y Rudnicki, W. R. (2010). Feature Selection with the Boruta Package. Journal of Statistical Software, 36(11), 1-13. https://doi.ora/10.18637/iss.v036. iH

Lasso, E., Corrales, D. C., Avelino, J., de Melo Virginio Filho, E. y Corrales, J. C. (2020). Discovering weather periods and crop properties favorable for coffee rust incidence from feature selection approaches. Computes and Electronics in Agriculture, 176, 105640. https://doi.ora/https://doi.ora/10.1016/j.com-pag.2020.105640

Li, H., Li, C. J., Wu, X. J. y Sun, J. (2014). Statistics-based wrapper for feature selection: An implementation on financial distress identification with support vector machine. Applied Soft Computing, 19, 57-67. https://doi. org/10.1016/j.asoc.2014.01.018

Li, J., Veeranampalayam-Sivakumar, A. N., Bhatta, M., Garst, N. D., Stoll, H., Stephen Baenziger, P., Belamkar, V, Howard, R., Ge, Y. y Shi, Y. (2019). Principal variable selection to explain grain yield variation in winter wheat from features extracted from UAV imagery. Plant Methods, 15(1), 123. https://doi.org/10.1186/s13007-019-0508-7

López-Ramírez, V., Ruíz, M., Rossi, E., Zuber, N., Lagares, A., Balzarini, M., Bonamico, N. y Fischer, S. (2022). Curtobacterium, a Foliar Pathogen Isolated from Mai-ze in Central Argentina. Current Microbiology, 79, 261. https://doi.org/10.1007/s00284-022-02953-y

Maldonado, S., Flores, Á., Verbraken, T., Baesens, B. y Weber, R. (2015). Profit-based feature selection using support vector machines - General framework and an application for customer retention. Applied Soft Computing, 35, 740-748. https://doi.org/10.1016/J. ASOC.2015.05.058

March, G. J., Balzarini, M., Ornaghi, J. A., Beviacqua, J. E. y Marinelli, A. (1995). Predictive model for “Mal de Río Cuarto” disease intensity. Plant Disease, 79(10).

Kuhn, M. (2021). Package “caret” Title Classification and Regression Training. . Consultado el 15 marzo de 2023. https://CRAN.R-project.ora/packaae=caret

Kuhn, M. y Silge, J. (2022). Tidy modeling with R. O'Reilly Media, Inc.

McEligot, A. J., Poynor, V., Sharma, R. y Panangadan, A. (2020). Logistic LASSO Regression for Dietary Intakes and Breast Cancer. Nutrients, 12(9), 2652. https://doi. org/10.3390/NU12092652

Nilsson, R., Peña, J. M., Bjorkegren, J. y Tegnér, J. (2007). Consistent Feature Selection for Pattern Recognition in Polynomial Time. The Journal of Machine Learning Research, 8, 589-612.

Paccioretti, P, Giannini-Kurina, F., Suarez, F. y Scavuzzo, M., Alemandri, V. M., Gómez Montenegro, B. y Balzarini, M. (2023). Protocolo para automatizar la descarga de datos climáticos desde la nube y generar indicadores biometeorológicos para el monitoreo epidemiológico de cultivos. AgriScientia, 40(1), 93-100. https://

doi.org/10.31047/1668.298x.v1.n40.39619 Peres, F. A. P. y Fogliatto, F. S. (2018). Variable selection methods in multivariate statistical process control: A systematic literature review. Computers & Industrial Engineering, 115, 603-619. https://doi.org/https://doi. org/10.1016/j.cie.2017.12.006 R Core Team (2022). R: A language and environment for statistical computing. In R Foundation for Statistical Computing. https://www.r-project.org/

Reyna, P, Suarez, F., Balzarini, M. y Pardina, P R. (2023). Influence of Climatic Variables on Incidence of Whi-tefly-Transmitted Begomovirus in Soybean and Bean Crops in North-Western Argentina. Viruses, 15(2), 462. https://doi.org/10.3390/V15020462 Rossi, E. A., Ruiz, M., Rueda Calderón, M. A., Bruno, C. I., Bonamico, N. C. y Balzarini, M. G. (2019). Meta-Analy-sis of QTL Studies for Resistance to Fungi and Viruses in Maize. Crop Science, 59(1), 125-139. https://doi. org/10.2135/CR0PSCI2018.05.0330

Rostami, M., Berahmand, K., Nasiri, E. y Forouzandeh, S. (2021). Review of swarm intelligence-based feature selection methods. Engineering Applications of Artificial Intelligence, 100, 104210. https://doi.org/https:// doi.ora/10.1016/j.enaappai.2021.104210

Ruiz, M., Rossi, E. A., Bonamico, N. C. y Balzarini, M. G. (2021). Modelos multivariados en la búsqueda de regiones genómicas para resistencia a mal de Río Cuarto y bacteriosis en maíz. BAG. Journal of Basic and Applied Genetics, 32(1), 25-33. https://doi. org/10.35407/BAG.2020.32.01.03

Rusyana, A., Notodiputro, K. A. y Sartono, B. (2021). The lasso binary logistic regression method for selecting variables that affect the recovery of Covid-19 patients in China. Journal of Physics: Conference Series, 1882(1), 012035. https://doi.org/10.1088/1742-6596/1882/1/012035

Shafiee, S., Lied, L. M., Burud, I., Dieseth, J. A., Alsheikh, M. y Lillemo, M. (2021). Sequential forward selection and support vector regression in comparison to LAS-SO regression for spring wheat yield prediction based on UAV imagery. Computers and Electronics in Agriculture, 183, 106036. https://doi.org/10.1016/J.COM-PAG.2021.106036

Shi, L., Westerhuis, J. A., Rosén, J., Landberg, R. y Brunius, C. (2019). Variable selection and validation in multivariate modelling. Bioinformatics, 35(6), 972-980. https://doi.org/10.1093/bioinformatics/bty710 Singh, K. (2021). Comparing Variable Selection Algo-rithms On Logistic Regression - A Simulation Tesis de Licenciatura, Uppsala University. DiVA, Uppsala University Library.

Suarez, F. M., Bruno, C. I., Giannini Kurina, F, Giménez Pecci, M. de la P., Rodríguez Pardina, P y Balzarini, M. (2023). Selecting Climatic Variables to Model Plant Di-sease Risk. SSRN Electronic Journal, 4314562. https:// doi.org/10.2139/SSRN.4314562

Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267-288.

Tikhonov, A. N. (1963). On the solution of ill-posed problems and the method of regularization. Doklady Aka-demii Nauk, 151(3), 501-504.

Vu, D. H., Muttaqi, K. M. y Agalgaonkar, A. P. (2015). A variance ¡nflation factor and backward elimination based robust regression model for forecasting monthly electricity demand using climatic variables. Applied Energy, 140, 385-394. https://doi.ora/10.1016/j.ape-nergy.2014.12.011

Whittingham, M. J., Stephens, P. A., Bradbury, R. B. y Freckleton, R. P. (2006). Why do we still use stepwise modelling in ecology and behaviour? Journal of Animal Ecology, 75(5), 1182-1189. https://doi.org/10.1111/ j.1365-2656.2006.01141.x

Wilches Ortiz, W. A., Vargas Diaz, R. E. y Espitia Malagón, E. M. (2022). Efectos del clima y su relación con el tizón tardío (Phytophthora infestans (Mont.) de Bary) en cultivo de papa (Solanum tuberosum L.). Siembra, 9(2), e4008. https://doi.org/10.29166/SIEMBRA. V9I2.4008

Witten, I. H., Frank, E., Hall, M. A. y Pal, C. J. (2016). Data Mining: Practical Machine Learning Tools and Techniques. The Morgan Kaufmann Series in Data Management Systems.

Yin, J., Mutiso, F y Tian, L. (2021). Joint hypothesis teting of the area under the receiver operating characteristic curve and the Youden index. Pharmaceutical Statistics, 20(3), 657-674. https://doi.org/https://doi. org/10.1002/pst.2099

ogata-Siudem, B. y Jaroszewicz, S. (2021). Fast stepwise regression based on multidimensional indexes. Information Sciences, 549, 288-309. https://doi.org/https:// doi.ora/10.1016/j.ins.2020.11.031

Zou, H. y Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society Series B: Statistical Methodology, 67(2), 301-320. https://doi.ora/10.1111/j.1467-9868.2005.00503.x